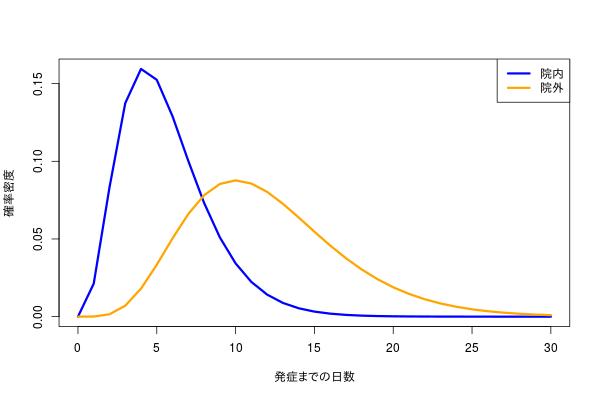
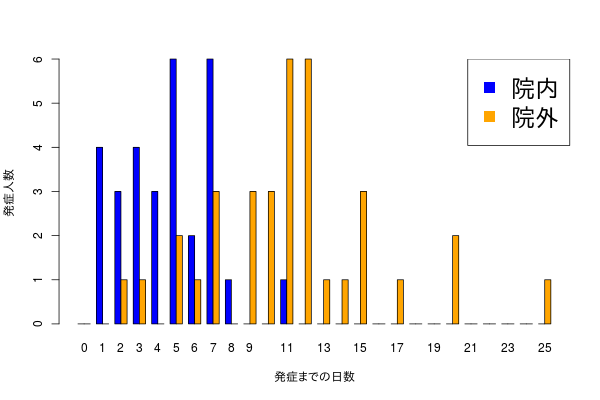
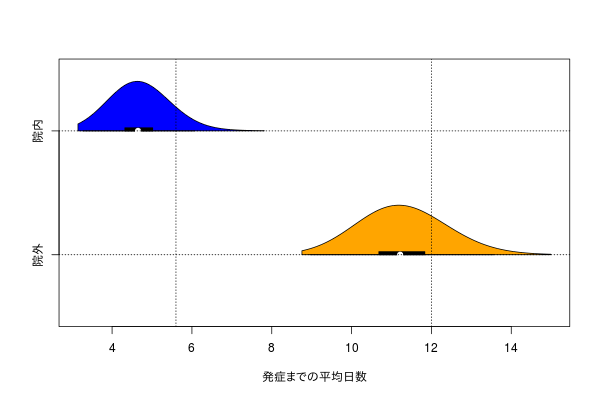
こんな感じのデータを見かけた。

本人が言うには、8日あたりを境目にして、8日までに発症するパターンと、それ以降に発症するパターンに分かれそうだ、という。
データの意味合いと二峰性の具合から、おそらくふたつのガンマ分布が重なっているのでは、という気分になった。というのも、横軸が0以上の整数値となる分布はガンマ分布で、混合分布として解けばたぶんふたつのパターンがそもそもどれくらいの存在比で、かつ、ガンマ分布で近似されれば各々のパターンの発症平均日が推定できるので、たぶんうれしい。
実際のデータはこの2つの分布から生成された。
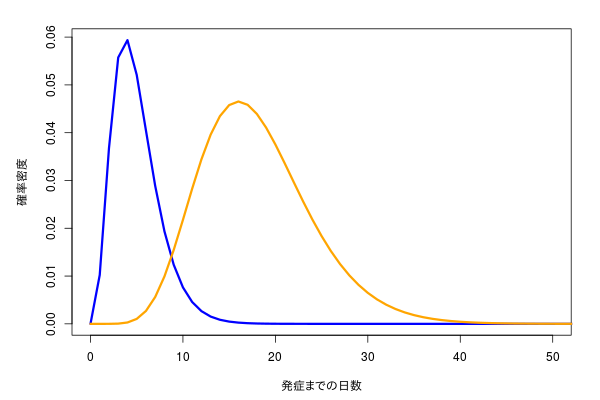
というわけで混合分布の推定で調べると、よく出てくるのはEMアルゴリズムとベイズである。
グダグダやっていたのだが、Rのパッケージで簡単にガンマ分布(というか混合分布全般)をEMアルゴリズムで推定してくれるやつがあった。
kusanagi.hatenablog.jp
mixtools というパッケージ内でgammamixEM という関数がEMアルゴリズムをしているが、ベクトル化されていない部分があるので適当にパクって書き換える。
初期値の設定としては、混合比 はディリクレ分布から適当に拾う。一様分布でも0.5 ずつでもよい。
はディリクレ分布から適当に拾う。一様分布でも0.5 ずつでもよい。
ガンマ分布にはshape と呼ばれる と、scale もしくはrate (shape の逆数)と呼ばれる
と、scale もしくはrate (shape の逆数)と呼ばれる のパラメータを設定する必要がある。mixtools では初期値の設定として、観測データ
のパラメータを設定する必要がある。mixtools では初期値の設定として、観測データ があるときに
があるときに をsort したあとに均等に分割して、分割されたセット
をsort したあとに均等に分割して、分割されたセット に対して(以下では表記の簡便化のため
に対して(以下では表記の簡便化のため は
は のつもりである)
のつもりである)



 (
( の分母と表記を合わせるために逆数にしてrate 表記にしている)
の分母と表記を合わせるために逆数にしてrate 表記にしている)
と設定している。
パラメータの収束は以下のようになる。ふたつの分布があるという前提なので、初期値次第では入れ替わる。この場合は色が入れ替わっているのでそうなる。
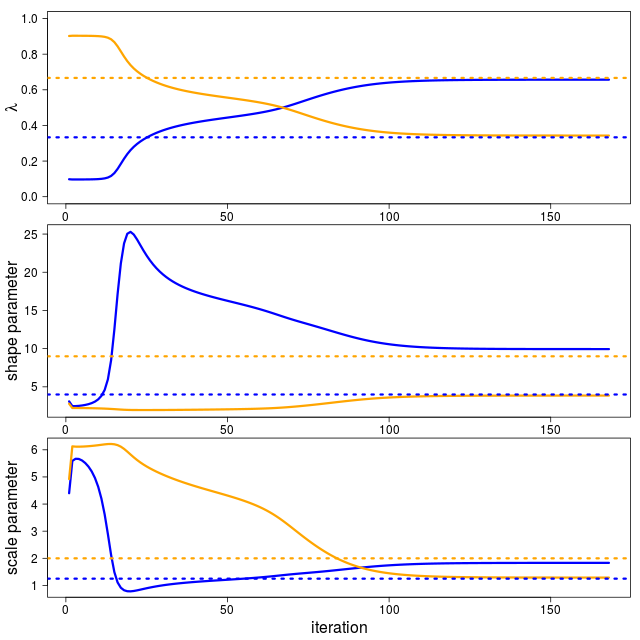
パラメータ的にはずれているように見えるが、分布としてしまうと意外とずれていないようである。
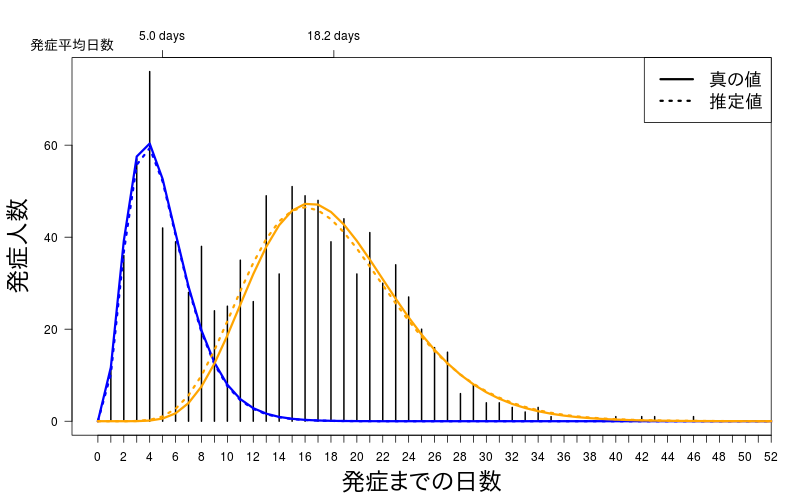
このときのパラメータの推定値は
$shape
[1] 3.859840 9.942502
$rate
[1] 0.7749822 0.5455689
$pi
[1] 0.3431185 0.6568815
それぞれの分布の平均値は
[1] 4.980553 18.224100
同様のことをstanを使ってやっている。
stan のマニュアルにゼロ過剰モデルなどあるので、いろいろパクってgamma_lpdf でtarget すると書ける。
stan でやるとパラメータの点推定値のみが得られるが、サンプリング過程でたくさんのパラメータを得るので、信頼区間(というか信用区間だが)っぽいものも得られる。
バイオリンプロットのside パラメータで片側だけ描けるというのがわかった。かつての努力はいったいなんだったんだろうか。
mikuhatsune.hatenadiary.com
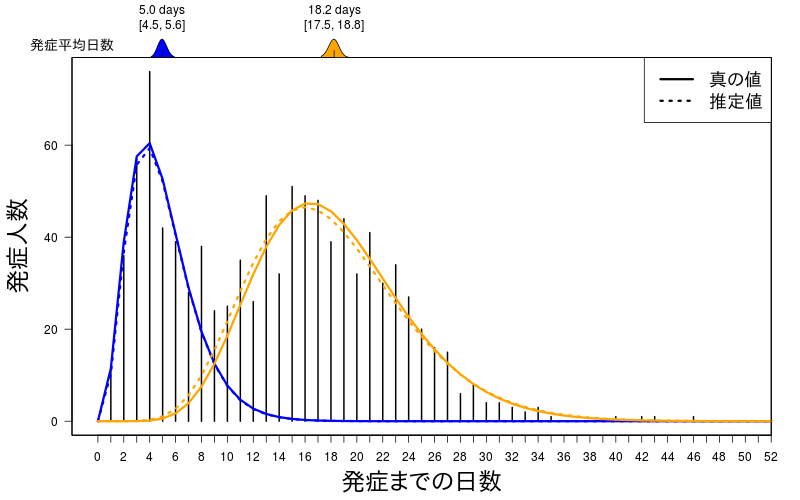
このときのパラメータの推定値は
$shape
[1] 3.896891 9.949112
$rate
[1] 0.7848028 0.5453568
$pi
[1] 0.3413815 0.6586185
それぞれの分布の平均値は
[1] 4.96544 18.24331
発症する平均日数の95%信用区間は
[,1] [,2]
2.5% 4.453284 17.54821
97.5% 5.559489 18.79025
ただし、stanでやるときは複数のchain を使うと、分布が入れ替わる問題で が収束しないのでchain はひとつでやった。解決策を知りたい。
が収束しないのでchain はひとつでやった。解決策を知りたい。
x <- 0:100
n <- 1000
shape <- c(4, 9)
rate <- c(0.8, 0.5)
mix <- c(1, 2)
p <- mix/sum(mix)
d <- t(mapply(dgamma, x, list(shape), list(rate)) * p)
xl <- c(0, 50)
cols <- c("blue", "orange")
par(mar=c(4.5, 5, 2, 2))
matplot(x, d, type="l", xlim=xl, xlab="発症までの日数", ylab="確率密度", col=cols, lty=1, lwd=3)
y <- sample(x, size=n, prob=rowSums(d), replace=TRUE)
EMgamma <- function(dat, k=2, eps=10e-8, maxit=300, seed=1234){
set.seed(seed)
idx <- sample(1:k, size=length(dat), replace=TRUE)
x.bar <- tapply(dat, idx, mean)
x2.bar <- tapply(dat^2, idx, mean)
theta <- thetas <- c(x.bar^2/(x2.bar - x.bar^2), (x2.bar - x.bar^2)/x.bar)
lambda <- lambdas <- c(MCMCpack::rdirichlet(1, rep(1, k)))
dens1 <- t(mapply(dgamma, dat, shape=list(head(theta, k)), scale=list(tail(theta, k))) * lambda)
ll <- old.obs.ll <- sum(log(rowSums(dens1)))
gamma.ll <- function(theta, z, lambda, k) -sum(z * log(t(mapply(dgamma, dat, shape=list(head(theta, k)), scale=list(tail(theta, k))) * lambda)), na.rm=FALSE)
diff <- 1 + eps
iter <- 0
while (diff > eps && iter < maxit) {
dens1 <- t(mapply(dgamma, dat, shape=list(head(theta, k)), scale=list(tail(theta, k))) * lambda)
z <- dens1/rowSums(dens1)
lambda.hat <- colMeans(z)
out <- try(suppressWarnings(nlm(gamma.ll, p = theta, lambda = lambda.hat, k = k, z = z)), silent = TRUE)
theta.hat <- out$estimate
new.obs.ll <- sum(log(colSums(mapply(dgamma, dat, shape=list(head(theta.hat, k)), scale=list(tail(theta.hat, k))) * lambda.hat)))
diff <- new.obs.ll - old.obs.ll
old.obs.ll <- new.obs.ll
ll <- c(ll, old.obs.ll)
lambda <- lambda.hat
lambdas <- rbind(lambdas, lambda)
theta <- theta.hat
thetas <- rbind(thetas, theta)
iter <- iter + 1
}
rownames(thetas) <- NULL
rownames(lambdas) <- NULL
return(list(theta=thetas, theta.hat=theta.hat, lambda=lambdas, lambda.hat=lambda.hat, ll=ll))
}
out <- EMgamma(y, k=2, seed=123)
lwd <- 3
par(mfcol=c(3, 1), mar=c(1, 5, 1.2, 1), cex.lab=2, cex.axis=1.5, las=1)
matplot(out$lambda, type="l", lty=1, col=cols, xlab="iteration", ylab=expression(lambda), ylim=c(0, 1), lwd=lwd)
abline(h=p, lty=3, col=cols, lwd=lwd)
par(mar=c(1, 5, 1.2, 1))
matplot(out$theta[, 1:k], type="l", lty=1, ylab="shape parameter", col=cols, lwd=lwd)
abline(h=shape, lty=3, col=cols, lwd=lwd)
par(mar=c(4.5, 5, 1.2, 1))
matplot(out$theta[, (2*k-1):(2*k)], type="l", xlab="iteration", ylab="scale parameter", lty=1, col=cols, lwd=lwd)
abline(h=1/rate, lty=3, col=cols, lwd=lwd)
pars <- list(shape=head(out$theta.hat, 2), rate=1/tail(out$theta.hat, 2), pi=out$lambda.hat)
pars$rate <- switch(which.min(pars$shape), pars$rate, rev(pars$rate))
pars$pi <- switch(which.min(pars$shape), pars$pi, rev(pars$pi))
pars$shape <- switch(which.min(pars$shape), pars$shape, rev(pars$shape))
est <- t(mapply(dgamma, x, list(pars$shape), list(pars$rate)) * pars$pi)
alpha <- 0.05
me <- pars$shape / pars$rate
library(vioplot)
b <- table(factor(y, x))
par(mar=c(4.5, 5, 4, 2), las=1, cex.lab=2)
plot(b, xlim=xl, xlab="発症までの日数", ylab="発症人数",)
for(i in seq(ncol(est))){
lines(x, est[, i]*n, lwd=3, col=cols[i])
lines(x, d[, i]*n, lwd=3, col=cols[i], lty=3)
}
axis(3, at=me, labels=sprintf("%.1f days", me), padj=0)
text(par()$usr[1], par()$usr[4], "発症平均日数", xpd=TRUE, pos=3, cex=1.2)
legend("topright", legend=c("真の値", "推定値"), lty=c(1, 3), lwd=3, cex=1.5)
library(rstan)
rstan_options(auto_write=TRUE)
options(mc.cores=parallel::detectCores())
code <- "
data {
int<lower=0> N;
int<lower=0> y[N];
}
parameters {
real<lower=0, upper=20> shape[2];
real<lower=0, upper=10> rate[2];
simplex[2] pi;
}
model {
real ps[2];
for(n in 1:N){
ps[1] = log(pi[1]) + gamma_lpdf(y[n] | shape[1], rate[1]);
ps[2] = log(pi[2]) + gamma_lpdf(y[n] | shape[2], rate[2]);
target += log_sum_exp(ps);
}
}
"
m0 <- stan_model(model_code=code)
standata <- list(N=length(y), y=y)
fit <- sampling(m0, standata, iter=1000, warmup=300, chain=1)
ex <- extract(fit, pars=c("shape", "rate", "pi"))
mes <- ex$shape/ex$rate
pars <- lapply(ex, apply, 2, median)
pars$rate <- switch(which.min(pars$shape), pars$rate, rev(pars$rate))
pars$pi <- switch(which.min(pars$shape), pars$pi, rev(pars$pi))
mes <- switch(which.min(pars$shape), mes, mes[,rev(seq(ncol(mes)))])
pars$shape <- switch(which.min(pars$shape), pars$shape, rev(pars$shape))
est <- t(mapply(dgamma, x, list(pars$shape), list(pars$rate)) * pars$pi)
alpha <- 0.05
me <- pars$shape / pars$rate
mes.ci <- apply(mes, 2, quantile, c(alpha/2, 1-alpha/2))
library(vioplot)
b <- table(factor(y, x))
par(mar=c(4.5, 5, 4, 2), las=1, cex.lab=2)
plot(b, xlim=xl, xlab="発症までの日数", ylab="発症人数",)
for(i in seq(ncol(est))){
lines(x, est[, i]*n, lwd=3, col=cols[i])
lines(x, d[, i]*n, lwd=3, col=cols[i], lty=3)
vioplot(mes[,i], at=par()$usr[4], add=TRUE, horizontal=TRUE, wex=10,
rectCol=NA, colMed=NA, lineCol=NA,
side="right", xpd=TRUE, col=cols[i])
}
axis(3, at=me, labels=sprintf("%.1f days\n[%.1f, %.1f]", me, mes.ci[1,], mes.ci[2,]), padj=-0.5)
text(par()$usr[1], par()$usr[4], "発症平均日数", xpd=TRUE, pos=3, cex=1.2)
legend("topright", legend=c("真の値", "推定値"), lty=c(1, 3), lwd=3, cex=1.5)