2017-01-18

指数分布族

R 形・動き機械学習統計数学

変数 $x$ , パラメータ $\theta$ があるとき、
$\begin{align}f(x|\theta)&=h(x)g(\theta)\exp\{\eta(\theta)T(x)\}\\&=h(x)\exp\{\eta(\theta)T(x)-A(\theta)\}\\&=\exp\{\eta(\theta)T(x)-A(\theta)+B(x)\}\end{align}$
と表すことができる場合は、指数分布族という。ここで、exp やlog で無理やりカッコ内に指数法則を使って変換してやれば、各々の式は同じことを意味している。
ここで、
$T(x)$ ：十分統計量 sufficient statistics
$\eta(\theta)$ ：natural parameter
指数分布族のwiki にはどんな分布が指数分布族で、統計量がどういうものかが書いてある。
　
ここでは、ベルヌーイ分布が指数分布族である例を出していて、
$\begin{align}p(x|\theta)&=\theta^x (1-\theta)^{1-x}\\&=\exp\{x\log\theta+(1-\theta)\log(1-\theta)\}\\&=(1-\theta)\exp\{x\log\frac{\theta}{1-\theta}\}\\&=\exp\{x\log\frac{\theta}{1-\theta}-(-\log(1-\theta))\}\end{align}$
となるので、
$T(x)=x$
$\eta(\theta)=\log\frac{\theta}{1-\theta}$
$A(\theta)=-\log(1-\theta)$
である。
十分統計量 $T(x)$ の期待値や分散を求めることができて、こちらやこちら(PDF)を使って例えばベルヌーイ分布の平均は
$\begin{align}E(T(x))&=\frac{A^{'}(\theta)}{\eta^{'}(\theta)}\\&=\frac{\frac{1}{1-\theta}}{\frac{1}{\theta}+\frac{1}{1-\theta}}\\&=\theta\end{align}$
となって $\theta$ であることが確認できる。' は微分である。
　
情報幾何の先生といろいろやっていて、分布をlog で変換した時にたぶんこれが有用ようなという雰囲気。

2016-12-07

球面調和関数の回転

R 形・動き Python 数学

MikuHatsune2016-12-07

球面調和関数をRでやったりPythonでやったりしていたのだが、球面調和関数展開して係数をもっているときに、物体が回転してしまうとルジャンドル関数が回転してしまうので、係数も回転に応じて適当に変換しないといけない。
これはたいてい、回転後のパラメータがカンマつきで表すと
$f(\theta^{'},\phi{'})=\sum_{l=0}^\infty \sum_{m{'}=-l}^l c_l^{m^{'}} Y_l^{{'}}(\theta{'},\phi{'})$
という、回転後の係数 $c_l^{m^{'}}$ で考えないといけない。ちなみに回転は、オイラー角 $(\alpha, \beta, \gamma)$ で、zyz 軸がどの教科書や論文をみてもそうかいてある。
回転自体はこれがわかりやすい。
　
回転しても、もとの係数 $c_l^m$ から計算できるように偉い人が考えていて、
$c_l^{m^{'}}=\sum_{m=-l}^l D_{l}^{m^{'},m} c_l^m$
$D_l^{m^{'},m}=e^{im\gamma}d_l^{m^{'},m}(\beta)e^{im\alpha}$
$d_l^{m^{'},m}(\beta)=\sum_{t=max(0,m-m^{'})}^{min(l+m,l-m^{'})} (-1)^t \frac{\sqrt{(l+m)!(l-m)!(l+m^{'})!(l-m^{'})!}}{(l+m-t)!(l-m^{'}-t)!(t+m^{'}-m)!t!}(\cos\frac{\beta}{2})^{2l+m-m^{'}-2t}(\sin\frac{\beta}{2})^{2t+m^{'}-m}$
とすごいことになっている。
R でがんばってみたが、計算は遅いし結果もおかしいしで、Python に頼る。pyshtools はもともとfortran でshtools というものがあるっぽいのだが、それのPython 用モジュールである。例を参考にやってみる。

import pyshtools as p
import numpy as np
import math
import itertools

pi = math.pi

# 球面調和関数係数をおさめる箱を適当につくる
x = p.SHCoeffs.from_random([10, 1, 0])
x.get_coeffs()

lmax = 2
x = p.SHCoeffs.from_zeros(lmax)
ls = [0, 1, 1, 1, 2, 2, 2, 2, 2]     # l の番地
ms = [0, -1, 0, 1, -2, -1, 0, 1, 2]  # m の番地
value = [10, 1, 2, 0, 1, 5, 3, 4, 0] # (l, m) の値

# sphericalharmonics coefficients
for (l, m, v) in zip(ls, ms, value):
  x.set_coeffs(v, l, m)

x.get_coeffs() でnumpy array float 型のリストを取得できる。 $l=2$ のデータを作ってみると、長さ2、中身はl+1 * l+1 次元の行列になっている。

array([[[ 10.,   0.,   0.],
        [  2.,   0.,   0.],
        [  3.,   4.,   0.]],

       [[  0.,   0.,   0.],
        [  0.,   1.,   0.],
        [  0.,   5.,   1.]]])

リストの最初は $m\geq 0$ の項で、2つめは $m<0$ の項である。ひとつめのリストには、 $l=0,1,2$ の要素がはいっていて、各 $l$ のリストには $m=0,1,2$ の要素が入っている。
$m<0$ のほうは少し変わっていて、各 $l$ のなかに $m=0,-1,-2$ の順番で要素がはいっている。要素をいじるにはset_coeffs() で値、 $l$ , $m$ の番地を指定すれば任意にいじることができる。
係数を取り出したかったら

def shc_extract(coef, lmax):
  c = [coef.get_coeffs()[0][0][0]]
  for i in range(1, lmax+1):
    for k in [1, 0]:
      if k == 0:
        for j in range(k, i+1):
          c += [coef.get_coeffs()[k][i][j]]
      else:
        for j in reversed(range(k, i+1)):
          c += [coef.get_coeffs()[k][i][j]]
  return c

shc_extract(x_rot, lmax)

　
球面調和関数は球面上のポテンシャルの(数学的には厳密な)級数展開なので、球面上のなにかを比較したかったら、係数を比較してもいいことになっている。もとの形を球面調和関数で記述してあるとして、適当にぐるぐる回転してみて、もっとも近いもしくは遠い回転を探してみる。
たぶんこれも、何かいい方法があるのだろうが、愚直に回転させまくってみる。10度ずつの回転をzyz に対して総当りする。総当りにはitertools が使い勝手がよく、めっちゃ速い。ちなみに上でzip を使って一括iterate しているが、これもパクっている。
　

div = 10                  # 何度ずつ回転するか
degs = range(1, 360, div) # 回転角度
rot_res = []
for i, j, k in itertools.product(degs, degs, degs):
  irad, jrad, krad = i*pi/180, j*pi/180, k*pi/180 # 回転角度をradian で記録しておく
  x_rot = x.rotate(irad, jrad, krad, degrees=False)
  rot_res += [[irad, jrad, krad, shc_extract(x_rot, lmax)]]


# R じゃないといろいろできない情弱なのでファイルに書き出す
w0 = open("rotate_shc.txt", "w")
for z in rot_res:
  txt = " ".join(map(str, z[:3])) + " " + " ".join(map(str, z[3])) + "\n"
  w0.write(txt)

w0.close()

　
実際は単位球面上に模様のように色が付いているが、その値に応じて半径を決めると、球面調和関数で画像をググったときにでてくるようなチョウチョみたいなアレができる。
差が最小の時の係数の回転である。ほとんど重なっているように見えるが、これでも(321, 1, 41)度回転しているらしい。

　
差が最大の時の係数の回転である。このときは(51, 161, 131)度回転している。

　
回転自体は、どれくらい細かくグリッドサーチするかと、 $d_l^{m,m^{'}}$ が $O(l^3)$ のオーダーで計算量がかかるらしいので、 $d_l^{m,m^{'}}$ を再帰的に求める方法もあるらしい。
Journal of Computational Physics 228(16):5621-5627 September 2009
　
$d_l^{m,m^{'}}$ を計算したかったらdjpi2 という関数が使える。これを使うと、最終的な回転はrotate 関数でできるが、

alpha = pi/8
beta = pi/9
gamma = pi/10
ang = [pi/1.2, pi/1.8, pi/3]
dj = p.shtools.djpi2(lmax)

x_rot = p.shtools.SHRotateRealCoef(x.get_coeffs(), np.array(ang), dj)
# 同じ
x_rot = x.rotate(alpha, beta, gamma, degrees=False)

とやっても同様な結果が得られる。

2016-11-05

ガウス混合分布と曲率等高線を用いたセグメンテーション

医学形・動き数学

MikuHatsune2016-11-05

読んだ。
Accurate Automatic Detection of Densely Distributed Cell Nuclei in 3D Space.
PLoS Comput Biol. 2016 Jun 6;12(6):e1004970.
プレスリリース
　
線虫の細胞の3D(4Dもいけるけど)画像のなかで、細胞がくっついているように見えるのもがうまくセグメンテーションされる、というもの。
細胞は蛍光で識別されており、細胞中心ほど濃く画像として認識される。複数の細胞が密集している場合に、光度の分布を考えて、その等高線の曲率をとると、細胞のくっついている領域がくびれとしてとれる。既存の方法よりかなり精度がいいようである。
線虫は発生における細胞の個数が決まっており、すべての細胞が追跡できれば捗る。
　
著者らはmatlab とImageJ を組み合わせて、アルゴリズムによるセグメンテーション後、GUI で好きにいじれるパッケージというか実装を公開しているのでこれをやったらクッソ落とし穴にハマったのでメモ。
~~というか、これで再現できるのかあやしい~~
　
環境はubuntu 14.04 LTS
Intel C++ compiler
Intel Parallel Studio XE が必要。ubuntu 14.04 には2013 が必要なので、うっかり2017とかDL してしまうとOS 要件で16.04 しか満たしてないけど? って怒られる。
これがないと icc ができない。
　
Fiji
Fiji (Nat Methods. 2012 Jun 28;9(7):676-82.) はImageJ の生物学的イメージング研究用にカスタマイズされたプラグインみたいなものである。これを取ってくる。

Download Fiji (Life-Line version, 2013 July 15) for appropriate operating system from web
(http://imagej.net/Fiji/Downloads) and decompress it.
Add (FIJI_INSTALL_DIR)/scripts to the matlab search path.
Copy lib/MorphoLibJ-1.0.7.jar and lib/roiedit3d_subclass/roiedit3d_subclass.jar to
(FIJI_INSTALL_DIR)/plugins.
MorphoLibJ is also available from github (https://github.com/ijpb/MorphoLibJ/releases).

とあるが、これはあとでmatlab でコマンドを打てばどうにかなる。
ここで、後にpeak_detection12 を実行するときにMarkerControlledWatershedTransform3D がないと怒られるのだが、これはFiji からプラグインを拡張しなければならず、こちらを参考にして

The Marker-controlled Watershed plugin is part of the MorphoLibJ library. To install it, you just need to add the IJPB-plugins update site:
1) Select Help ▶ Update... from the Fiji menu to start the updater.
2) Click on Manage update sites. This brings up a dialog where you can activate additional update sites.
3) Activate the IJPB-plugins update site and close the dialog. Now you should see an additional jar file for download.
4) Click Apply changes and restart Fiji.
You should now find the plugin under the sub-menu Plugins ▶ MorphoLibJ ▶ Segmentation.
Note: Marker-controlled Watershed is only one of the plugins included in the MorphoLibJ suite. By following these installation steps, you will be installing as well the rest of plugins in the suite.

とする。
また、lib/roiedit3d_subclass/roiedit3d_subclass.jar のなかにはMyTableModel がはいっているので、これをjavaaddpath する必要がある。
　
matlab のインストール
この実装にはmatlab がないとどうしようもない。matlab は有料だが30日間なら無料トライアルができる。
MathMorks から大学アカウントとかいれてダウンロードするが、すべてをインストールするとこれだけで10GB とか消費するので、必要な

Image Processing Toolbox, Statistics and Machine Learning Toolbox, and Optimization Toolbox

で4GB くらい容量がいる。
今回はR2016b をインストールしたので、.matlab/R2016a とか変なものがあれば削除して、.matlab/R2016b/ を作る。
　
elipsoid_em_12.mexa64 の作成
minmaxfit はいいが、elipsoid のほうは単純にicc すればいいかというとそうでもなかった。
まず、パスが通っていなければ$MATLAB_ROOT を定義しておく。今回の私の環境では以下である。

MATLAB_ROOT="/usr/local/MATLAB/R2016b/"

次に、icc かなにかのコンパイルでヘッダーinclude が足りないと言われるので、c++/4.8 を入れる。

icc -c elipsoid_em_12.cpp -DMKL_ILP64 -fPIC -debug expr-source-pos -ftz -xHost -I$MATLAB_ROOT/extern/include -I$MKLROOT/include /usr/include/x86_64-linux-gnu/c++/4.8/ -O3 -fp-model fast=2 -DNDEBUG -opt-matmul -axAVX -static -openmp-stubs

その後、リンクコマンドというものをやるが、これをただやるだけだとリンクされないようなので、libirng.so がどうたらこうたら言われる。そこで、intel compiler ライブラリ周りでのエラーを参考に、管理者権限(sudo)で

cd /etc/ld.so.conf.d
vim intel_compiler.conf

vim で下記ファイルを作成して

/opt/intel/composer_xe_2013/lib/intel64/

読み込む。

ldconfig

とすると、リンクができているようである。これを言っている通り、mexa64 ファイルをsrc ディレクトリに移動させる。
　
やっていると、ImageJ で大きいデータを読み込むときに、よく java heap error みたいなことを言われる。これはmatlab のGUI からヒープ時の対応を参考に、適当に大きい値をいれる。
　
matlab とImageJ とjavaclasspath の恒久的な設定がアレなので、matlab 上で一時的に追加するならばこんな感じでmat.m ファイルを作っておいて、起動する度に読み込め(実行すれ)ばよい。
というのも、matlab GUI からこの解析を実行すると死ぬほど止まったり挙動がおかしくなったりするので、強制終了をなんかいもせざるを得ない。
また、MyFileInfoVirtualStack というものをここから入手して作成しないといけないのだが、まず、MyFileInfoVirtualStack.java を実行するときにij.jar の類がないと怒られるので、ImageJ のソースを落としてきて、ij.jar があるディレクトリを classpath オプションで追加する。

cd ~/Desktop/software/software/src/
addpath('~/Fiji.app/scripts/')
javaaddpath('/home/username/Desktop/getSubImage-master/')
javaaddpath('/home/username/Desktop/software/software/lib/roiedit3d_subclass/')

　
解析したいTIF ファイルはSSBD もしくはfigshare にデータが投稿されているから、peak_detection_12_param.txt と同ディレクトリにいれてmatlab からpeak_detection_12 と roiedit3d を実行する。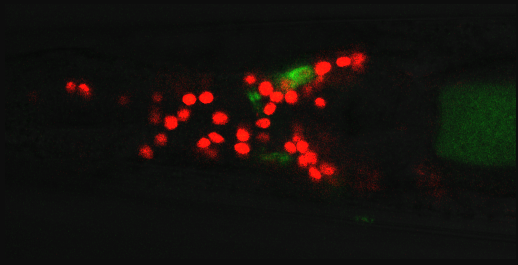
　
Reproducible research とはいったい()

2016-09-18

球面調和関数をR でやる

R Rpackage 形・動き数学

MikuHatsune2016-09-18

球面調和関数をrPython でやっていたが、R だけで完結するほうが、rPython に投げてやりとりするより圧倒的に高速かつ安定なので、頑張ってR でやった。
ゴールとしては、
$f(\theta, \phi)=\sum_{l}^{\infty}\sum_{m=-l}^lc_l^m Y_l^m$
となる係数 $c_l^m$ を求めることだが、これはルジャンドル陪関数が直交するという性質を利用して
[tex:c_l^m=] (内積)
を求めることでなんとかなる。
degree $l$ は理想的には無限大まで行けば、 $f(\theta, \phi)$ は完璧に級数展開されるが、現実的には30か40くらいまでいけば、たいていの形は再現されるっぽいようなことが論文によく書いてあるから、 $L_{max}=25$ くらいまでがんばった。
　
orthopolynom というパッケージで、ルジャンドル関数までは用意してくれるが、 $m$ 階の微分は自分で用意しないといけない。
実際に3次元物体を扱うには実数部分が必要だから、sph1 関数で最終的に必要な実部もしくは虚部だけ取ってくる。

library(orthopolynom)
l <- 5
m <- 2
theta <- pi/7
phi <- pi/8
p_l_m <- function(l, m){ 
  legp <- legendre.polynomials(l)[l+ 1]
  for(mm in 1:m){
    legp <- polynomial.derivatives(legp)
  }
  polynomial.coefficients(legp)[[1]]
}
p_l_m <- function(x, l, m){
  legp <- legendre.polynomials(l)[l+1]
  polynomial.values(eval(parse(text=paste0(paste(rep("polynomial.derivatives(", abs(m)), collapse=""), "legp", paste(rep(")", abs(m)), collapse=""))))[1], x)[[1]]
}

sph <- function(theta, phi, l, m){
  x <- cos(theta)
  y <- cos(m*phi) + 1i*sin(m*phi)
  #Plm <- (-1)^m * (1-x^2)^(m/2)*p_l_m(x, l, m)
  Plm <- sin(theta)^abs(m)*p_l_m(x, l, m)
  #res <- (-1)^((m+abs(m))/2)
  res <- (-1)^((m+abs(m))/2)*Plm*sqrt((2*l+1)/4/pi*factorial(l-abs(m))/factorial(l+abs(m)))*y
  return(res)
}

sph1 <- function(theta, phi, l, m){
  s <- sph(theta, phi, l, m)
  ifelse(rep(m, length(s)) >= 0, Re(s), Im(s))
}

$Y_0^0=\frac{1}{\sqrt{4\pi}}$ だから確かめると、合ってる。

sph1(0.5, 0.5, 0, 0)

[1] 0.2820948

1/sqrt(4*pi)

[1] 0.2820948

　
単位球面上に均一な点を発生させて、 $f(\theta,\phi)=1$ ができるかどうか検算してみる。gss というオブジェクトが単位球で、SphericalCubature パッケージのrect2polar 関数で極座標に変換できる。

library(rgl)
library(geometry)
library(SphericalCubature)
# フィボナッチ数を返す関数
FN <- function(n){
	# 負の数のフィボナッチ数は、正のそれに符号をつけたもの
	if(n<0){
		return(both.fn.3(-n)*(-1)^(n+1))
	}
	# 0,1,2はフィボナッチ数発生の種なので指定する
	if(n==0){
		return(0)
	}else if (n==1 | n==2){
		return(1)
	}else{# 3以上は、計算する
		tmp <- rep(0,n)
		tmp[1] <- tmp[2] <- 1
		for(i in 3:n){
			tmp[i] <- tmp[i-1]+tmp[i-2]
		}
		return(tmp[length(tmp)])
	}
}

# 球面らせん法
# f1は黄金比
fib.lattice.S2 <-function(N,f1=(sqrt(5)+1)/2,k=1){
	f2 <- f1-1 # 黄金比はx^2-x-1=0の１つの根。もう１つの根を取り出す
	# 点の数2N+1
	P <- 2*N+1
	# -N から Nまでの整数列
	i <- seq(from=-N, to=N,by=k)
	# zの座標は-1 から 1の均等割り
	theta <- asin(2*i/(2*N+1))
	z <- sin(theta)
	# そのようなz座標に対応する、(x,y)座標を取り出すにあたり
	# 黄金比から作ったf2に応じてxy平面での角座標を作る
	phi <- 2*pi*i*f2
	# その角を使って、z座標に対応した半径の座標とする
	x <- cos(theta)*cos(phi)
	y <- cos(theta)*sin(phi)
	return(cbind(x,y,z))
}
# FN(n)個の点をつくるために、引数をFN(n)/2とする
gss <- fib.lattice.S2(FN(18)/2)
rad <- rect2polar
rad <- t(rect2polar(t(gss))$phi)

# l はLmax まで、m は -l, ..., 0, ..., l までひたすら計算する。
Lmax <- 25
ylm <- function(theta, phi, Lmax) mapply(function(l) mapply(function(m) sph1(theta, phi, l, m), -l:l), 0:Lmax)

# theta, phi に対応して ylm を計算する
# 計算結果は、m+1 番目のリストに、(theta, phi) の組の数だけの行と
# -l, ..., 0, ..., l の列の行列
w <- ylm(rad[,1], rad[,2], Lmax)

# 係数は内積で得られる
coef <- function(vec, Y) mapply(function(z) c(vec %*% z), Y)
# 単位球なので f(theta, phi)=1 である
a <- coef(rep(1, nrow(rad)), w)

# あるm について、-l ~ l まですべて足す
# その後、m についても足す
r <- 4*pi*rowSums(sapply(mapply(function(z1, z2) sweep(z1, 2, z2, "*"), w, a), rowSums)

# ひとつの頂点が担当している球面上の領域は、均一なので頂点数で割ればいいはず
r <- r/nrow(gss)

hist(r)

　
ほとんど1なのでよい。

　
しかし、spin transform した球でやると、球面上で密もしくは疎な部分があり、そこの頂点は担当する球面面積がいろいろ違うので、適当に補正する必要があるのだが、面積比で補正してもうまくいかなかったのでちょっと直さないといけない。

2016-09-03

離散型物体データの球面調和関数展開

R 形・動き形・動き Python Rを使いこなす数学医学

MikuHatsune2016-09-03

球面調和関数を使って.obj データを級数展開してくれるやつを後輩が書いてくれたのでやってみる。
例えばこれ(J Med Syst. 2014 May;38(5):20.)では、病気の肝臓と健康な肝臓をCT画像から構成して、球面調和関数による比較分類を行っている。
肝硬変が進んだ病気の肝臓は、線維化といって見た目がカチカチのゴツゴツになる。臨床的には辺縁(エッジ)が鈍と言ったり、ミクロには肝表面に再生結節というブツブツができたりする。
CT画像から肝臓の形を再構成したはいいが、物体同士の比較をするのに球面調和関数で級数展開しておく。degree $l$ とorder $m$ によって球面調和関数が決まる。ただし、 $l$ が小さすぎると大雑把にしかならない。次元の高い $L_{max}$ は物体表面の細かい正確さを決めているとされる。

Fig.5 からパクった。 $L_{max}$ が大きくなるとより肝臓っぽくなる。この論文では以前の報告から $L_{max}=15$ でよさそうと決めている。他に、医学方面で球面調和関数を使っている論文は例えば脳MRI とかだが、12 から25 くらいでやっていることが多そう。
ただし、 $L_{max}$ をひたすら大きく取れば物体細部の分解能が上がるかというとそうではないっぽくて、例えば球面調和関数は $\sum_{l}^{L_{max}}\sum_{m=-l}^{l}$ で計算されるから、 $L_{max}$ ひとつにつき計算されるorder $m$ が ${L_{max}}^2=\sum(2L_{max}-1)$ となる(球面調和関数の展開図がピラミッド状に表現されていることからわかる)。
　
球面調和関数の係数はspintransformation の最後に吐き出される仕様になっている。球面調和関数自体はR ではやるのが面倒くさそうなのでこれまたrPython でゴリ押しする。
$L_{max}=9$ くらいでそれ以上は細かいところがグダグダになるようなのでここが限界のようだが、かといって元のうさぎが表現できているかというとあやしい。
　

元リンクのサンプル。
　

元のスタンフォードうさぎ

$L_{max}=2$

$L_{max}=6$

$L_{max}=9$

$L_{max}=15$

$L_{max}=20$

$L_{max}=25$

library(rgl)
library(geometry)
library(SphericalCubature)
d <- read.table("bunny.obj") # とりあえずスタンフォードうさぎ
d0 <- split(d[,-1], d[,1])
m0 <- tmesh3d(t(d0$v), t(d0$f), homogeneous=FALSE)

# 球面調和関数の係数データ
sh_coef <- as.numeric(strsplit(readLines("coef.txt"), " ")[[1]])
library(rPython)

# Python で球面調和関数を計算できるようにおまじない
python.exec("import numpy as np")
python.exec("from scipy.special import sph_harm as _sph_harm")
python.exec("
def sph_harm(l, m, theta, phi):\
  if m >= 0:\
    return np.sqrt(2) * _sph_harm(m, l, phi, theta).real\
  else:\
    return np.sqrt(2) * _sph_harm(-m, l, phi, theta).imag")

# 球面調和関数の係数を与えて元の物体の級数展開をゴリ押しする
python.exec("
def SH(Lmax, c, u, v):\
  r = np.zeros([len(u), len(v)])\
  for l in range(Lmax + 1):\
    for m in range(-l, l + 1):\
      r += c[l**2 + l + m] * sph_harm(l, m, np.array(u, ndmin=2).T, v).real\
  \
  return map(list, r)")

# 球面座標用の theta, phi
u <- seq(0, 180, length=80)*pi/180 # u = np.linspace(0, np.pi, 80)
v <- seq(0, 360, length=60)*pi/180 # v = np.linspace(0, 2 * np.pi, 60)

# 元リンクのデータを再現するなら
cvec <- c(10, 1, 2, 0, 1, 5, 3, 4, 0)

# rPython でPython に投げてゴリ押しする
r <- c(do.call(rbind, python.call("SH", 2, sh_coef, u, v)))

x <- r*c(outer(sin(u), cos(v)))
y <- r*c(outer(sin(u), sin(v)))
z <- r*c(outer(cos(u), rep(1, length(v))))
xyz <- cbind(x, y, z)
Z <- convhulln(xyz/r)
m1 <- tmesh3d(t(xyz), tmesh3d(t(xyz/r), t(Z), homogeneous=F)$it, homogeneous=FALSE)
open3d()
shade3d(m1, col="grey")
rgl.viewpoint(30, 20, zoom=0.8)
movie3d(spin3d(axis=c(0, 1, 0)), duration=12, fps=5)

2016-07-19

球面調和関数をrPython でやる

R Python LINUX 形・動き Rpackage Rを使いこなす数学

MikuHatsune2016-07-19

球面調和関数をやりたいがRではいいものがないのでPythonでやった結果をrPython を使ってRでゴリ押し計算するやり方。R を投げ捨ててPython に移行したかったが、結局R でやっちゃう。
rPython について知りたければ下にスクロール。
　
球面上の離散的な分布をなんらかの関数で級数展開できれば、関数化できる。球面上の分布 $f$ は、球座標表示で $f(\theta, \phi)$ と書ける。これを、ルジャンドル多項式
$P_l(x)=\frac{1}{2^n n!}\frac{d^l}{dx^l}(x^2-1)^l$
とルジャンドル陪関数
$P_l^m(x)=(-1)^m(1-x^2)^{\frac{m}{2}}\frac{d^m}{dx^m}P_l(x)$
を用いて、球面調和関数
$Y_l^m(\theta, \phi)=(-1)^{\frac{m+|m|}{2}}\sqrt{\frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}}P_l^{|m|}(\cos\theta)exp(im\phi)$
と表すことができる。虚数が入っているので、実数版は
$Y_l^m=\{\begin{matrix}\sqrt{2}(-1)^mRe(Y_l^m)&if\hspace{3}m>0\\Y_l^0&if\hspace{3}m=0\\\sqrt{2}(-1)^{-m}Im(Y_l^{-m})&if\hspace{3}m<0\end{matrix}$
となる。
l はdegree, m はorder とよく書かれている。 $-l\leq m \leq l$ である。
　
Rでは球面調和関数を直接やってくれそうな関数がなさそうなので、組み合わせてやってみる。orthopolynom パッケージはルジャンドル多項式を返す。結果は0 degree からl degree まで出力される。

library(orthopolynom)
l_spharm <- 5 # l; degree
m_spharm <- 0 # m; order
legp <- legendre.polynomials(l_spharm)

[[1]]
1 

[[2]]
x 

[[3]]
-0.5 + 1.5*x^2 

[[4]]
-1.5*x + 2.5*x^3 

[[5]]
0.375 - 3.75*x^2 + 4.375*x^4 

[[6]]
1.875*x - 8.75*x^3 + 7.875*x^5

legendre.polynomials は直接微分してくれる。複数回の微分(m) はその都度loop を回す。

l_spharm <- 5 # l; degree
m_spharm <- 2 # m; order
legp <- legendre.polynomials(l_spharm)[l_spharm + 1]
for(mm in 1:m_spharm){
  legp <- polynomial.derivatives(legp)
}

[[1]]
-52.5*x + 157.5*x^3

さてここで、具体的なルジャンドル倍関数を求めて確かめてみる。
$P_2^2(x)=-3(1-x^2)$ なので、

l_spharm <- 2 # l; degree
m_spharm <- 2 # m; order
legp <- legendre.polynomials(l_spharm)[l_spharm + 1]
for(mm in 1:m_spharm){
  legp <- polynomial.derivatives(legp)
}
P_l_m <- function(x) sum((-1)^m_spharm * (1-x^2)^(m_spharm/2) *polynomial.coefficients(legp)[[1]]* x^(0:(l_spharm-m_spharm)))

x <- seq(-1, 1, length=100)
plot(x, mapply(P_l_m, x))
#lines(x, -3*x*sqrt(1-x^2)) # l <- 2; m <- 1
lines(x, 3*(1-x^2))

確かにあってる。

　
本当なら、球面調和関数同士の積、内積がクロネッカーのデルタ $\delta_{l,l^{'}}$ になることを利用して、もとの球面上の関数 $f(\theta,\phi)$ は
$f(\theta,\phi)=\sum_{l=0}^\infty\sum_{m=-l}^lc_l^mY_l^m(\theta,\phi)$
$c_l^m=\int_{-{\pi}}^{\pi} d\phi\int_0^{\pi} d\theta \sin\theta f(\theta, \phi)Y_l^m(\theta, \phi)$
となる。
が、全然うまくRで再現できない。
上のリンクでわざわざPython コードがあるので、これを再利用することを考える。R からPython を利用するには、rPython パッケージを使う。
入らない場合は

sudo apt-get install python-dev

# これはPython
import numpy as np
from scipy.special import sph_harm as _sph_harm
def sph_harm(l, m, theta, phi):
    return _sph_harm(m, l, phi, theta)

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import matplotlib.cm as cm

# R^2(u=θ, v=Φ)
u = np.linspace(0, np.pi, 80)
v = np.linspace(0, 2 * np.pi, 80)

# R^3
x = np.outer(np.sin(u), np.cos(v))
y = np.outer(np.sin(u), np.sin(v))
z = np.outer(np.cos(u), np.ones(v.size))

fig = plt.figure()
Lmax = 3
for l in range(Lmax + 1):
    for m in range(-l, l+1):
        # 球面調和関数の値を色で表す
        sph = np.abs(sph_harm(l, m, np.array(u, ndmin=2).T, np.array(v)))
# 正規化
#        if sph.max() == sph.min():
#            sph.fill(0.5)
#        else:
#            sph = (sph - sph.min()) / (sph.max() - sph.min())
        colors = cm.jet(sph) #cm.bwr
        ax = fig.add_subplot(Lmax + 1, 2*Lmax+1, l*(2*Lmax+1)+m+Lmax+1, projection="3d")
        ax.set_axis_off()
        surf = ax.plot_surface(x, y, z, facecolors=colors,
                rstride=2, cstride=2, linewidth=10, shade=False)

plt.savefig("sh_c.png", transparent=False)

rPython には4つの関数しかない。しかし、Python ができるのであればこれらの関数だけで十分強力な武器になる。
python.assign はPython へオブジェクトを定義する。

a <- 1:4
python.assign( "a", a )

python.exec はPython 上で演算を実行する。代入もできる。

python.exec( "b = len(a)" )

python.get はPython 上で定義されているオブジェクトを取り出す。ただし、Python でのarray 配列などはR に持ち込んだ時にJSON がウンタラカンタラ言われるので、Python 上でlist にしてR に吐き出すのがいいのかもしれない。

python.get("b")

python.call はPython 上の関数に、R から引数をいれて計算させる。python.assign でいちいちPython になげてやってもいいけれども、面倒だったらpython.exec でPython 上に好きに関数を定義してしまえばR から解決できる。

a <- 1:4
b <- 5:8
python.exec( "def concat(a,b): return a+b" )
python.call( "concat", a, b)

Python でライブラリを持っていれば、実行できる。

python.exec( "import math" )
python.get( "math.pi" )

さて、RでできないことをPython でゴリ押ししよう。scipy 内に球面調和関数を計算してくれるやつがあるので、これをそのまま読み込む。
リンクではlとm, $\theta$ と $\phi$ が逆なのでゴニョゴニョしているが、R で書く行が増えるのでいい感じに帳尻を合わせる。
Python で1行のものはそのままpython.* で挟めばよい。

# R で
# rPython
python.exec("import numpy as np")
python.exec("from scipy.special import sph_harm as _sph_harm")

Python はインデント構造にうるさいので、タブインデントをひたすら横に書いた長い行をいれてもよいが、見栄えを大切にするなら改行コマンドをいれる。
元のコードが

# Python
def sph_harm(l, m, theta, phi):
  sph = np.abs(_sph_harm(m, l, np.array(phi), np.array(theta, ndmin=2).T))
  return [list(d0) for d0 in sph]

ゴリ押しすると

# R
python.exec("def sph_harm(l, m, theta, phi):\
  sph = np.abs(_sph_harm(m, l, np.array(phi), np.array(theta, ndmin=2).T))\
  return [list(d0) for d0 in sph]")

また、上の実部だけ取り出すやつも、元のコードが

# Python
def sph_harm(l, m, theta, phi):
  if m > 0:
      sph = np.sqrt(2) * (-1)**m * _sph_harm( m, l, np.array(phi), np.array(theta, ndmin=2).T).real
  if m == 0:
      sph = _sph_harm(m, l, np.array(phi), np.array(theta, ndmin=2).T).real
  else:
      sph = np.sqrt(2) * (-1)**m * _sph_harm(-m, l, np.array(phi), np.array(theta, ndmin=2).T).imag
  return [list(d0) for d0 in sph]

ゴリ押しすると

# R
python.exec("def sph_harm(l, m, theta, phi):\
  if m > 0:\
      sph = np.sqrt(2) * (-1)**m * _sph_harm( m, l, np.array(phi), np.array(theta, ndmin=2).T).real\
  if m == 0:\
      sph = _sph_harm(m, l, np.array(phi), np.array(theta, ndmin=2).T).real\
  else:\
      sph = np.sqrt(2) * (-1)**m * _sph_harm(-m, l, np.array(phi), np.array(theta, ndmin=2).T).imag\
  return [list(d0) for d0 in sph]")

これで、R上からm, l, $\theta$ , $\phi$ を与えればPython で球面調和関数を計算して、あたかもR でやってくれたようにできる関数ができたので、確かめる。

# R^2(u=θ, v=Φ)
# パラメータ
u <- seq(0, 180, length=180)*pi/180 # u = np.linspace(0, np.pi, 80)
v <- seq(0, 360, length=360)*pi/180 # v = np.linspace(0, 2 * np.pi, 60)

# プロット用の xyz
x <- c(outer(sin(u), cos(v)))
y <- c(outer(sin(u), sin(v)))
z <- c(outer(cos(u), rep(1, length(v))))
xyz <- cbind(x, y, z)

l <- 6
m <- 6

# ここで rPython の利用
# sph_harm は実数部分版
sph <- python.call("sph_harm", l, m, u, v) # u length list and v length vector
sph <- unlist(sph)
cuti <- 20
cols <- greenred(cuti)[cut(sph, quantile(sph, seq(0, 1, length=cuti + 1)))]

plot3d(xyz, col=cols)
zz <- t(polar2rect(abs(sph), t(expand.grid(v, u)[,2:1])))
plot3d(zz, col=cols)

　
ubuntu14.04, R3.3.0, Python 2.7.1 なので他OS では未確認。

2016-07-14

球面上に均等な点を配置したい

R 形・動き数学

MikuHatsune2016-07-14

球面上に均一な点を配置したい。約N個ならばこんな感じでやれるが、厳密にN 個おきたい。
実装が簡単なこれをやってみる。
　
そもそも、なぜ均一な点を球面上に配置したいかというと、基準点集合として扱えるからである。計算機では3次元データは離散的に持っており、ある球面上の点と別の物体の球面上の点を比較したいときに、両者で揃っていて、なおかつ有限個でありながら無数の点があれば離散でも連続っぽく扱えるため、比較がなんとかできるようになる。だから均一な点をたくさん発生させたい。
　
しかしながら、数学的に厳密な球面上の均一配置は不可能である。正多面体を考えて、その頂点に点を配置させれば、厳密に均一な点が配置できるが、正多面体は四、六、八、十二、二十に限られているので、たくさん均一な点を置きたいときには不便である。
球面上にランダムに点を発生させたときは、球面全体で見れば均一だが、局所的には疎だったり密だったりするのでこれまたよくない。メルカトル図法っぽく格子を作っても、北南極ではグシャっと潰れるのでこれもこの部分の均一性がよろしくない。
というわけでらせんを使うらしい。
球面座標系 $f(\theta, \phi, r=1)$ に全部で $N$ 個の均一な点を球面上に発生させる。ことを考える。螺旋のスタートとゴールは北極と南極ということにする。すなわち、 $\theta_{1}=\pi, \theta_{N}=0$ であり、 $\phi_1=0$ とする。 $k$ 番目の点にたいして、
$h_k=2\frac{k-1}{N-1}-1$
として、
$\theta_{k}=acos{h_k}$
$\phi_{k}=\phi_{k-1}+\frac{3.6}{\sqrt{N}}\frac{1}{\sqrt{1-{h_k}^2}}=\phi_1+\frac{3.6}{\sqrt{N}}\sum\frac{1}{\sqrt{1-{h_k}^2}}$
が、均一な点の角度となる。
こうしても、厳密な均一ではない。というのも、北極と南極の歪みがあるからである。これを適当に補正するために、 $\{2,3,5,6,7\}$ と $\{N-1,N-2,N-4,N-5,N-6\}$ の均一点ベクトルの平均をとって適当に変えてやる。
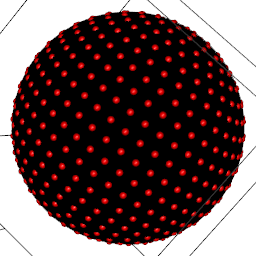
すると、緑の点が黄色になって、極での均一さがちょっとマシになる。
geometry パッケージのconvhulln を使えば、凸包をして簡単に球状オブジェクトができる。

library(rgl)
library(SphericalCubature)
a <- seq(-90, 90, length=200)*pi/180
b <- seq(-180, 180, length=300)*pi/180
r <- 1
rad <- expand.grid(b, a)

GSS <- function(N=600, r=1){
  hk <- 2*((2:N)-1)/(N-1) - 1
  theta_k <- c(pi, acos(hk))
  phi_k <- 0
  for(k in 2:N){
    phi_k <- c(phi_k, tail(phi_k, 1) + 3.6/sqrt(N)/sqrt(1-hk[k-1]^2))
  }
  phi_k[N] <- phi_k[N-1] + 3.6/sqrt(N)
  # phi_k <- c(0, 3.6/sqrt(N)*mapply(function(z) sum(1/sqrt(1-replace(hk, N-1, 0)[1:z]^2)), 1:(N-1))) # slower
  gss <- t(polar2rect(rep(1, N), rbind(theta_k, phi_k)))
  gss[1,] <- colMeans(gss[c(2, 3, 5, 6, 7),])
  gss[N,] <- colMeans(gss[N-c(1, 2, 4, 5, 6),])
  return(gss)
}

xyz <- t(polar2rect(rep(1, nrow(rad)), t(rad)))
gss <- t(polar2rect(rep(1, N), rbind(theta_k, phi_k)))
cols <- replace(rep("red", N), c(1, N), "green")
plot3d(xyz)
spheres3d(gss, col=cols, radius=0.03)

convhulln(GSS())