時系列データにt 検定を行うことに関してstan 神の解析がやばい

時系列データにt 検定を行うことに関して、すごいもにょっていたのだが、そもそもstan 神が既にモデル化してくれていた。
リンクでは2階差分と、変化点検出のコーシー分布の合わせ技を用いている。
そのままパクってやってみる。

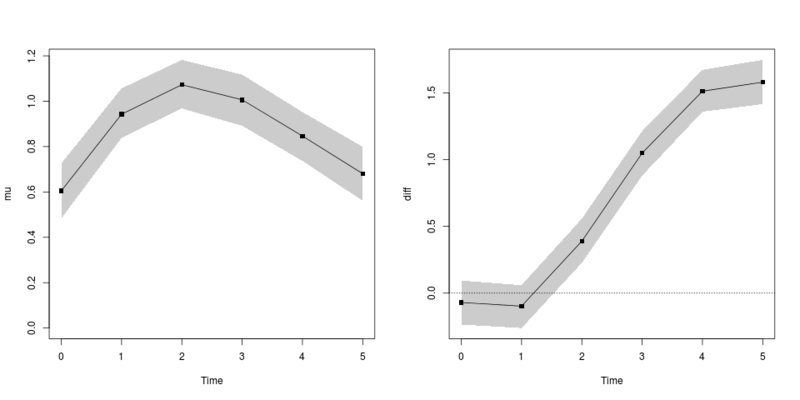
diの95%ベイズ信頼区間が0を含んでいない期間が差がある期間と言えるでしょう。さらに、どこから差がありそうなのか、どれほど差がありそうなのかも確率付きで述べることができます。

ということが、stan による柔軟なモデリングで述べることができます。
　
話は飛ぶけど、読んだ。

はじめての 統計データ分析 ―ベイズ的〈ポストp値時代〉の統計学―

書評はまた書くけれども、この時系列データと同じように、この本では、例えば分散分析や分割用を用いて、「どことどこが比較して差があるか」という、実際のデータ解析でも気になる点を実例を用いて解説してくれている。
古典的なp値検定では、この問に答えることはクッソ難しかったが、ベイズだとかなり柔軟に対応できるようになるので、いいと思います。

# berobero.stan
data {
  int N_time;
  int N0;
  int N1;
  vector[N_time] Y0[N0];
  vector[N_time] Y1[N1];
}

parameters {
  vector[N_time] mu;
  real di0;
  vector<lower=-pi()/2, upper=pi()/2>[N_time-1] di_unif;
  real<lower=0> s_mu;
  real<lower=0> s_di;
  real<lower=0> s_Y;
}

transformed parameters {
  vector[N_time] di;
  vector[N_time] y1_mean;
  di[1] <- di0;
  for (t in 2:N_time)
    di[t] <- di[t-1] + s_di*tan(di_unif[t-1]);
  y1_mean <- mu + di;
}

model {
  for (t in 3:N_time)
    mu[t] ~ normal(2*mu[t-1] - mu[t-2], s_mu);
  for (n in 1:N0)
    Y0[n] ~ normal(mu, s_Y);
  for (n in 1:N1)
    Y1[n] ~ normal(y1_mean, s_Y);
}

# データ作り
x <- seq(0, 10, length=100)
d <- 0:5
n <- 10

b <- 0.5
g <- exp(-1/2.5)/exp(-1)
f0 <- function(x) ((x)^2)*exp(-x/1) + b
f1 <- function(x) ((x)^2)*exp(-x/2.5)/g + b

y0 <- replicate(n, f0(d) + rnorm(length(d), sd=0.2))
y1 <- replicate(n, f1(d) + rnorm(length(d), sd=0.2))
y01 <- list(y0, y1)

library(rstan)
standata <- list(N_time=length(d), N0=ncol(y01[[1]]), N1=ncol(y01[[2]]),
                 Y0=t(y01[[1]]), Y1=t(y01[[2]]))
stanmodel01 <- stan_model("berobero.stan")                 

fit0 <- sampling(stanmodel01, data=standata, chains=3, warmup=1000, iter=3000, seed=1234)
ex0 <- extract(fit0)

alpha <- 0.05
Y_ci <- t(apply(ex0$mu, 2, quantile, c(alpha/2, 1-alpha/2)))
Y_me <- apply(ex0$mu, 2, median)
yl <- range(0, Y_ci)

xp <- c(d, rev(d))
yp <- c(Y_ci[,1], rev(Y_ci[,2]))
matplot(d, Y_ci, type="n", xlab="Time", ylab="mu", ylim=yl)
polygon(xp, yp, col=grey(0.8), border=NA)
lines(d, Y_me, type="o", pch=15)

Y_ci <- t(apply(ex0$di, 2, quantile, c(alpha/2, 1-alpha/2)))
Y_me <- apply(ex0$di, 2, median)
yl <- range(0, Y_ci)

xp <- c(d, rev(d))
yp <- c(Y_ci[,1], rev(Y_ci[,2]))
matplot(d, Y_ci, type="n", xlab="Time", ylab="diff", ylim=yl)
polygon(xp, yp, col=grey(0.8), border=NA)
lines(d, Y_me, type="o", pch=15)
abline(h=0, lty=3)

共通のベースライン（mu；左図）と、変異体と野生型の差（di；右図）の結果。
時刻0, 1 の時点では差が出ないようにデータを作っていて、2 以降から差が出るようになっている。
また、シミュレーションの曲線では、緑の曲線が時刻 5 で頭打ちになるようにしていて、これもそれとなく推定されている。
個人的にはggplot2 が慣れていないから、これを描くスクリプトも載せてほしいな!!