3次元空間に拡張する

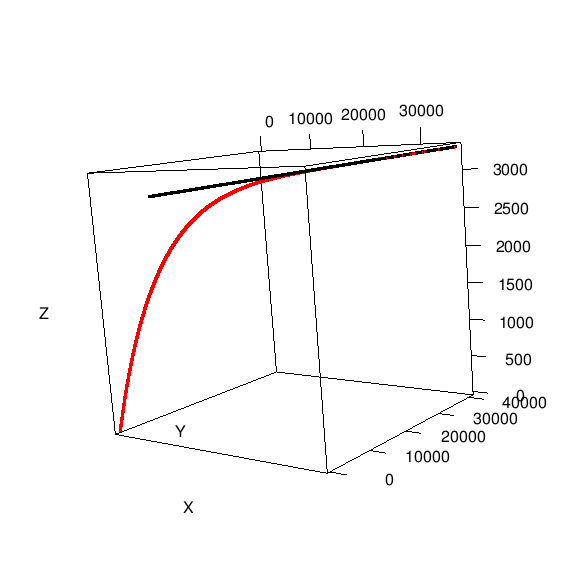
2次元平面から3次元平面でやってみたいと思った。
ただ、微分方程式的に解くのは難しそうだったので、シミュレーション的に計算してしまおう。
　
飛行機は初期位置から、速度で移動する。
ミサイルは初期位置から発射され、速度で飛行機を追尾する。
微小時間で、
飛行機：
ミサイル：
に変位する。このとき、ミサイルは飛行機を最短距離で捕捉するので、ミサイルの軌道に対して、接線方向に飛行機がいる。つまり、ミサイルの速度は方向ベクトルに平行である。
ミサイルの速さは一定だと仮定すると、適当な定数を用いてと書け、である。

#飛行機の初期位置
x0 <- 6000
y0 <- 5000
z0 <- 3000

vk_e <- c(100, 120, 1) #飛行機の速度ベクトル
vk <- sqrt(sum(vk_e^2)) #飛行機の速度ベクトルの大きさ

elapsed.time <- seq(0, 300, length=10000) #観察時間
dt <- diff(elapsed.time)[1] #シミュレーションの微小時間
ka60 <- missile <- matrix(0, nr=length(elapsed.time), nc=3,) #飛行機とミサイルの座標行列

#飛行機の位置についてシミュレーション
ka60[1, ] <- c(x0, y0, z0)
for(i in 2:length(elapsed.time)){
	delta <- vk_e * dt
	ka60[i, ] <- ka60[i - 1, ] + delta
}

um <- 1.2 * vk #ミサイルの速度ベクトルの大きさ。常に飛行機より一定倍大きいと仮定する。
#ミサイルの軌道についてシミュレーション。
for(j in 1:(length(elapsed.time) -1)){
	vec_e <- ka60[j, ] - missile[j, ]
	k <- um / sqrt(sum(vec_e ^ 2))
	missile_vec <- k * vec_e
	
	delta <- missile_vec * dt
	missile[j + 1, ] <- missile[j, ] + delta
}

library(rgl)
snake <- rbind(ka60, missile)
xyzlim <- apply(snake, 2, range)
colpalet <- rep(c("black", "red"), each=length(elapsed.time))
plot3d(snake, xlim=xyzlim[, 1], ylim=xyzlim[, 2], zlim=xyzlim[, 3], xlab="X", ylab="Y", zlab="Z", col=colpalet)