アレルとgenotype の頻度を信頼区間付で求めたい - 驚異のアニヲタ社会復帰の予備

という質問を受けたので1万年と2000年ぶりくらいに遺伝統計やった。
雰囲気としては、こんな感じの値を求めたい。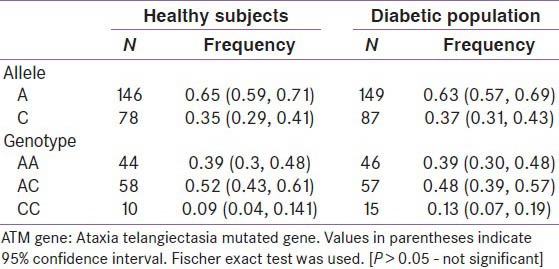

f:id:MikuHatsune:20190831141253j:plain — Indian J Endocrinol Metab. 2014 Nov-Dec; 18(6): 850–854. のTable 1 より引用

www.ncbi.nlm.nih.gov
　
ここで、データとしては被験者たちのgenotypeを実験により決定（genotypingという）して、AA 44人、AC 58人、CC 10人という結果を得た。
まず、このgenotypeの頻度については、 $x_{AA}$ , $x_{AC}$ , $x_{CC}$ がそれぞれ人数を表していて、表記上 $x_1$ , $x_{2}$ , $x_{3}$ と対応させて、なおかつ $x_1+x_2+x_3=n$ とする。
各genotype の頻度 $p_1$ , $p_2$ , $p_3$ は $p_i=\frac{x_i}{n}$ であるが、各genotype は多項分布からサンプリングされると仮定すると、多項分布の期待値は $np_i$ , 分散は $np_i(1-p_i)$ である。
信頼区間は $\mu\pm Z_{1-\frac{\alpha}{2}}\sqrt{\textit{Var}}$ で求められるが、genotype が少ないとT分布くらいにしておいたら良さそうなので

x1 <- c(MM=44, MN=58, NN=10)
x2 <- c(MM=46, MN=57, NN=15)

AlleleGenotypeFreqCalc(x1)$GenotypeFrequency

           Frequency    lowerCI   upperCI
MajorHomo 0.39285714 0.30142061 0.4842937
Hetero    0.51785714 0.42430584 0.6114084
MinorHomo 0.08928571 0.03589828 0.1426731

AlleleGenotypeFreqCalc(x2)$GenotypeFrequency

          Frequency    lowerCI   upperCI
MajorHomo 0.3898305 0.30092124 0.4787398
Hetero    0.4830508 0.39195381 0.5741479
MinorHomo 0.1271186 0.06639384 0.1878434

となりそれっぽくなった。
　
genotype は集団からgenotyping でデータを得られるが、実際に知りたいのはその元となったMとNが集団内にどれだけ存在しているかである。
遺伝学的には、MM、MN、NNの個体が交配することで、生物学的にはMとNを切り離し、確率的にはランダムで父方と母方のMもしくはNをもらうことで、次世代の個体のMMかMNかNNとなり、それが観測される。
MM、MN、NNの個体の数からMとNの数を推定するのは、HWEを利用すれば可能で、例えば
ここ（PDF)では、アレルの頻度 $p_M$ （小文字で、なおかつこのページの上部のgenotype の頻度で使った $p$ とは違うことに注意）は、genotype の頻度 $P_{MM}$ （大文字）より
$p_M=P_{MM}+\frac{1}{2}\displaystyle\sum_{M\neq N}^{} P_{MN}$
$p_M$ の分散は
$\textit{Var}(p_M)=\frac{1}{2n}(p_M+P_{MM}-2p_M^2)$ （小文字と大文字に注意）
になる。

AlleleGenotypeFreqCalc(x1)$AlleleFrequency

      Frequency   lowerCI   upperCI
Major 0.6517857 0.5939582 0.7096132
Minor 0.3482143 0.2903868 0.4060418

AlleleGenotypeFreqCalc(x2)$AlleleFrequency

      Frequency   lowerCI   upperCI
Major 0.6313559 0.5709773 0.6917345
Minor 0.3686441 0.3082655 0.4290227

library(HardyWeinberg)
alpha <- 0.05

AlleleGenotypeFreqCalc <- function(x=c(MM=44, MN=58, NN=10), alpha=0.05){
  HW.test <- HWChisq(x, verbose=FALSE)
  # アレル頻度
  AlleleFreq <- c(1-HW.test$p, HW.test$p)
  V2 <- (AlleleFreq + x[-2]/sum(x) - 2*AlleleFreq^2)/(2*sum(x))
  AlleleFreqCI <- cbind(AlleleFreq,
                        AlleleFreq-qnorm(1-alpha/2)*sqrt(V2),
                        AlleleFreq+qnorm(1-alpha/2)*sqrt(V2)
                       )
  rownames(AlleleFreqCI) <- c("Major", "Minor")
  colnames(AlleleFreqCI) <- c("Frequency", "lowerCI", "upperCI")
  # HWEからの頻度
  COV <- 2*V2[1]*(1+HW.test$f)
  GenotypeFreq <- c((1-HW.test$p)^2, 2*(1-HW.test$p)*HW.test$p, HW.test$p^2)
  GenotypeFreqCI <- cbind(GenotypeFreq,
                          GenotypeFreq-qnorm(1-alpha/2)*sqrt(COV),
                          GenotypeFreq+qnorm(1-alpha/2)*sqrt(COV)
                         )
  rownames(GenotypeFreqCI) <- c("MajorHomo", "Hetero", "MinorHomo")
  colnames(GenotypeFreqCI) <- c("Frequency", "lowerCI", "upperCI")
  # 多項分布からの頻度
  MultinomP <- x/sum(x)
  CI <- qt(1-alpha/2, sum(x))*sqrt(MultinomP*(1-MultinomP)/sum(x))
  MultinomFreq <- cbind(MultinomP, MultinomP-CI, MultinomP+CI)
  rownames(MultinomFreq) <- c("MajorHomo", "Hetero", "MinorHomo")
  colnames(MultinomFreq) <- c("Frequency", "lowerCI", "upperCI")
  return(list(input=x, AlleleFrequency=AlleleFreqCI, HWEFrequency=GenotypeFreqCI, GenotypeFrequency=MultinomFreq))
}

x1 <- c(MM=44, MN=58, NN=10)
x2 <- c(MM=46, MN=57, NN=15)
AlleleGenotypeFreqCalc(x1)
AlleleGenotypeFreqCalc(x2)