「男女間モテ格差」をzero-inflated model で考える - 驚異のアニヲタ社会復帰の予備

こんな話を見つけた。

そもそも、女性の考える「非モテ男性」と実際の「非モテ男性」の認識にすれ違いがありそう。

女性は何もしなくても75％は一度は告白される。
一方男性は、半数以上が一度も告白されない。

女性のリアルからみると「非モテ」とは「下位25％（＝特殊）」な「気持ち悪い人たち」なのかもしれない。 pic.twitter.com/wh79I5x59j
— すもも (@sumomodane) January 2, 2020

元ネタ、データはこちらにある。
note.com

データとしては、20代の男女各200人からアンケート調査によって、過去に告白したことがあるか、されたことがあるかその回数を聞いている。
ここで、

「過去告白した回数」よりも、「過去告白された回数」において大きな差があることが確認できる。特に「過去告白された回数」が「0回」における男女差が大きく、男性は51.5％と半数以上が告白されたことがないのに対して、女性は25.0％にとどまる。以上より分布の点から「男女間モテ格差」があることが確認できた。

とあり、
「過去告白された回数」が「0回」という非モテ（筆者注：ワイが言ってるだけで引用元ではない）がおおよそ男女で50%:25% という差がある。
この上で、

平均値をみると、「過去告白した回数」は男性1.66回、女性1.26回と男性の方が多い。一方、「過去告白された回数」は男性1.60回、女性3.03回と、女性の方が倍近く多い。平均値の点からも「男女間モテ格差」があることが確認できる。

とあるが、告白されるのは少なくとも非モテではない集団なので、告白される回数が0回の非モテ集団の告白される回数を足しあわせてそのまま集団の平均として出すのは、非モテでない人たちの告白される回数を過小評価する。
というわけで、非モテは告白されることはないので、この非モテ集団がアンケート調査内にどれだけいたかを推定して、非モテでない集団が通常どれくらい告白されるのかをきちんと推定してみたい。

となればzero-inflated model である。

zero-inflated model のstan コードはこちらにあるので、丸々パクってやってみる。
mc-stan.org
stan コード中の $\theta$ が非モテ集団の割合（二項分布のパラメータ）で、 $\lambda$ が非モテでない集団が平均して告白される回数（ポアソン分布のパラメータ）である。
引用元には告白する回数、される回数が男女別で割合が載っているが、サンプルサイズN=200, 告白する/される回数の水準がいくつか結合されているので、割合を参考に適当にリサンプリングして、引用元の平均値±0.01 に収まるシミュレーションデータをstan に投げる。ここで、告白10回以上は適当な予備実験の結果、最大15回ということにしておいた。target 記法で頑張ればここらへんはなんとかできそうな気がする。
がんばりたい人はこちらを読もう。

StanとRでベイズ統計モデリング (Wonderful R)

作者:松浦健太郎
出版社/メーカー: 共立出版
発売日: 2016/10/25
メディア: 単行本

リサンプリングしたデータはこのような感じになる。なお、回数を覚えていないというのは面倒なので除いた。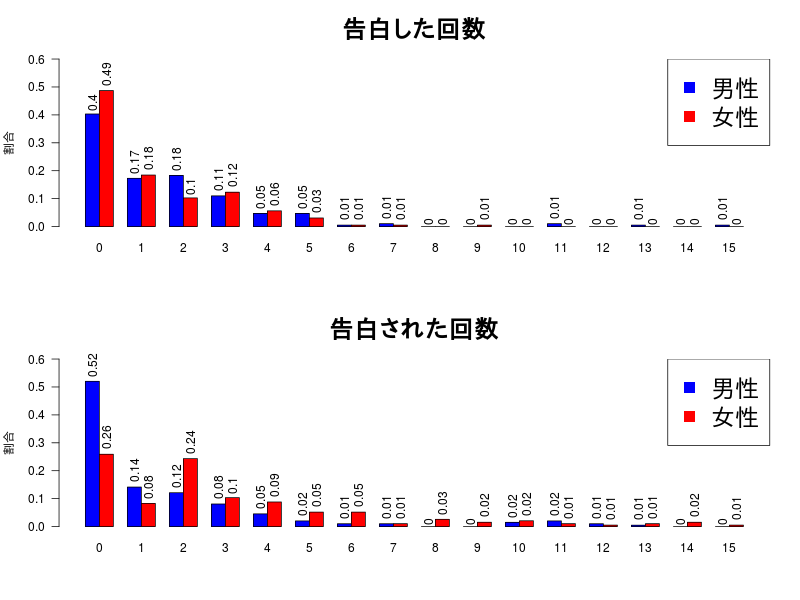

f:id:MikuHatsune:20200103195547p:plain — リサンプリングで作成したシミュレーションデータ

・告白した回数について
一度も告白したことのない男性は $\theta=0.35$ 、女性は $\theta=0.42$ (p=0.126) だった。
告白した回数については男性は $\lambda=2.57$ 回、女性は $\lambda=2.17$ 回 (p=0.04) だった。
告白をすることに関して非モテ（消極的?）は男女間で差はなさそうだが、非モテでない集団では男性のほうが告白回数は多いようである。ただし0.5回の多さが重大な差なのかは不明。

・告白された回数について
一度も告白されたことのない男性は $\theta=0.5$ 、女性は $\theta=0.25$ (p=0) だった。
告白された回数については男性は $\lambda=3.19$ 回、女性は $\lambda=4.02$ 回 (p=0.00083) だった。
告白されたことのない男性は女性にくらべてすごい多いようである。そもそも50%ってアンケート調査の半分だしこれってどうなん? 感はあるが、残りの半分100人でも推定はうまくいっている。
告白された回数については、ほぼ1回くらいの差がついた。

現実には4回告白される人が平均的に多い、とはちょっと考えにくいような気もするけれども、アンケート調査結果的には3-5回くらいが多いようなのでまあそうなのだろう。
ヤリチン理論的に、何十回も告白されるような最強のモテ男女が存在しそうな気がするが、200人のサンプルサイズでは補足できなかったのか。。。

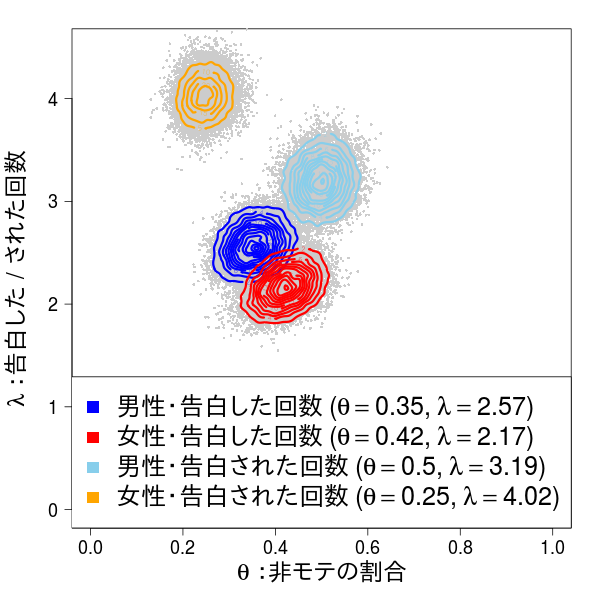
f:id:MikuHatsune:20200103195619p:plain — $\theta$ と $\lambda$

N <- 200 # サンプルサイズ

k <- list(c(0, 0), 1, c(2, 3), c(4, 5), 6:9, c(10:15))
u1 <- c(38.5, 16.5, 28.5, 9, 1.5, 2)/100 # 男性、告白した
u2 <- c(47.5, 18, 22, 8.5, 1.5, 0)/100  # 女性、告白した
p1 <- c(51.5, 14, 20, 6.5, 2, 5)/100 # 男性、告白された
p2 <- c(25, 8, 33.5, 13.5, 10, 6.5)/100 # 女性、告白された
up <- list(u1, u2, p1, p2)

me <- c(1.66, 1.26, 1.60, 3.03) # zero-inflated を考慮しない平均値
lm <- mapply(function(z) c(-1, 1)/100 + z, me, SIMPLIFY=FALSE)

# 分布をもとにリサンプリングでシミュレーションデータを作成する
# 10回以上の告白は、最大15として、適当にsample される確率に傾斜をかける
sim <- function(p){
  unlist(mapply(sample, k, size=p*N, replace=TRUE, prob=mapply(function(z) order(z, decreasing=TRUE)/(length(z)*(length(z)+1)/2), k)))
}

# iter 回データセットを作って
# zero-inflated model を考慮しない平均値に近いデータをsize 個採用することにする（計算時間の都合）
iter <- 15000
size <- 50
tmp <- mapply(function(z) replicate(iter, sim(z)), up)
tmp_m <- lapply(tmp, colMeans)
tmpTF <- mapply(function(z1, z2) z1[1] < z2 & z2 < z1[2], lm, tmp_m, SIMPLIFY=FALSE)
tmp <- mapply(function(z1, z2) z1[, z2], tmp, tmpTF)
dat <- mapply(function(z) z[, sample(ncol(z), size=size)], tmp, SIMPLIFY=FALSE)

# シミュレーションデータの例
cols <- c("blue", "red")
bar1 <- rbind(table(factor(dat[[1]][,1], 0:15)), table(factor(dat[[2]][,1], 0:15)))
bar2 <- rbind(table(factor(dat[[3]][,1], 0:15)), table(factor(dat[[4]][,1], 0:15)))


mf <- c("男性", "女性")
koku <- c("告白した回数", "告白された回数")
b0 <- list(bar1/rowSums(bar1), bar2/rowSums(bar2))
yl <- c(0, 0.6)
par(mfrow=c(2, 1), cex.main=2, las=1)
for(i in seq(b0)){
b <- barplot(b0[[i]], beside=TRUE, col=cols, ylab="割合", ylim=yl, main=koku[i])
for(j in seq(ncol(b))){
  for(l in 1:2){
    text(b[l, j], b0[[i]][l, j], round(b0[[i]][l, j], 2), srt=90, adj=c(-0.2, NA), xpd=TRUE)
  }
}
legend("topright", legend=mf, col=cols, pch=15, cex=2)
}

# 推定する
library(rstan)
rstan_options(auto_write=TRUE)
options(mc.cores=parallel::detectCores())

code <- "
data {
  int<lower=0> N;
  int<lower=0> y[N];
}
parameters {
  real<lower=0, upper=1> theta;
  real<lower=0> lambda;
}
model {
  for (n in 1:N) {
    if (y[n] == 0)
      target += log_sum_exp(bernoulli_lpmf(1 | theta),
                            bernoulli_lpmf(0 | theta)
                              + poisson_lpmf(y[n] | lambda));
    else
      target += bernoulli_lpmf(0 | theta)
                  + poisson_lpmf(y[n] | lambda);
  }
}
"

m0 <- stan_model(model_code=code)
fitres <- replicate(length(dat), vector("list", size), simplify=FALSE)
for(i in seq(fitres)){
  for(j in seq(size)){
    hoge <- dat[[i]][, j]
    standata <- list(N=length(hoge), y=hoge)
    fitres[[i]][[j]] <- sampling(m0, standata, iter=800, warmup=200)
  }
}

# theta とlambda だけとってくる
x <- lapply(fitres, lapply, extract, pars=c("theta", "lambda"))
X <- lapply(lapply(x, lapply, do.call, what=rbind), do.call, what=cbind)
est <- as.data.frame(t(sapply(X, apply, 1, median)))

# 男女の比較
mean(X[[1]][1,] > X[[2]][1,]) # 告白する、theta
mean(X[[1]][2,] > X[[2]][2,]) # 告白する、lambda
mean(X[[3]][1,] > X[[4]][1,]) # 告白される、theta
mean(X[[3]][2,] > X[[4]][2,]) # 告白される、lambda

# 密度分布をかく
library(MASS)
kd <- vector("list", length(fitres))
for(i in seq(kd)){
  x0 <- X[[i]][1,]
  y0 <- X[[i]][2,]
  kd[[i]] <- kde2d(x0, y0, c(bandwidth.nrd(x0), bandwidth.nrd(y0)), n=100)
}

xl <- c(0, 1)
yl <- c(0, 4.5)
cols <- c("blue", "red", "skyblue", "orange")
led <- c("男性・告白した回数", "女性・告白した回数", "男性・告白された回数", "女性・告白された回数")
sub <- sapply(seq(led), function(x) as.expression(substitute(z1~"("*theta==z2*","~lambda==z3*")", list(z1=led[x], z2=round(est$theta[x], 2), z3=round(est$lambda[x], 2)))))
par(mar=c(5, 5, 2, 2), cex.lab=2, cex.axis=1.5, las=1)
plot(0, type="n", xlim=xl, ylim=yl, xlab=substitute(theta~"：非モテの割合"), ylab=substitute(lambda~"：告白した / された回数"))
for(i in seq(kd)){
  points(X[[i]][1,], X[[i]][2,], pch=16, cex=0.5, col=grey(0.8))
}
for(i in seq(kd)){
  contour(kd[[i]], add=TRUE, col=cols[i], lwd=3)
}
legend("bottomright", legend=sub, col=cols, pch=15, cex=2.1)

legend に数式をいれるのに苦労した。
stackoverflow.com