球面上に均等な点を配置したい - 驚異のアニヲタ社会復帰の予備

MikuHatsune2016-07-14

球面上に均一な点を配置したい。約N個ならばこんな感じでやれるが、厳密にN 個おきたい。
実装が簡単なこれをやってみる。
　
そもそも、なぜ均一な点を球面上に配置したいかというと、基準点集合として扱えるからである。計算機では3次元データは離散的に持っており、ある球面上の点と別の物体の球面上の点を比較したいときに、両者で揃っていて、なおかつ有限個でありながら無数の点があれば離散でも連続っぽく扱えるため、比較がなんとかできるようになる。だから均一な点をたくさん発生させたい。
　
しかしながら、数学的に厳密な球面上の均一配置は不可能である。正多面体を考えて、その頂点に点を配置させれば、厳密に均一な点が配置できるが、正多面体は四、六、八、十二、二十に限られているので、たくさん均一な点を置きたいときには不便である。
球面上にランダムに点を発生させたときは、球面全体で見れば均一だが、局所的には疎だったり密だったりするのでこれまたよくない。メルカトル図法っぽく格子を作っても、北南極ではグシャっと潰れるのでこれもこの部分の均一性がよろしくない。
というわけでらせんを使うらしい。
球面座標系 $f(\theta, \phi, r=1)$ に全部で $N$ 個の均一な点を球面上に発生させる。ことを考える。螺旋のスタートとゴールは北極と南極ということにする。すなわち、 $\theta_{1}=\pi, \theta_{N}=0$ であり、 $\phi_1=0$ とする。 $k$ 番目の点にたいして、
$h_k=2\frac{k-1}{N-1}-1$
として、
$\theta_{k}=acos{h_k}$
$\phi_{k}=\phi_{k-1}+\frac{3.6}{\sqrt{N}}\frac{1}{\sqrt{1-{h_k}^2}}=\phi_1+\frac{3.6}{\sqrt{N}}\sum\frac{1}{\sqrt{1-{h_k}^2}}$
が、均一な点の角度となる。
こうしても、厳密な均一ではない。というのも、北極と南極の歪みがあるからである。これを適当に補正するために、 $\{2,3,5,6,7\}$ と $\{N-1,N-2,N-4,N-5,N-6\}$ の均一点ベクトルの平均をとって適当に変えてやる。
すると、緑の点が黄色になって、極での均一さがちょっとマシになる。
geometry パッケージのconvhulln を使えば、凸包をして簡単に球状オブジェクトができる。

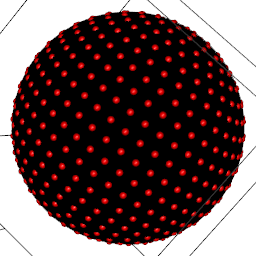
library(rgl)
library(SphericalCubature)
a <- seq(-90, 90, length=200)*pi/180
b <- seq(-180, 180, length=300)*pi/180
r <- 1
rad <- expand.grid(b, a)

GSS <- function(N=600, r=1){
  hk <- 2*((2:N)-1)/(N-1) - 1
  theta_k <- c(pi, acos(hk))
  phi_k <- 0
  for(k in 2:N){
    phi_k <- c(phi_k, tail(phi_k, 1) + 3.6/sqrt(N)/sqrt(1-hk[k-1]^2))
  }
  phi_k[N] <- phi_k[N-1] + 3.6/sqrt(N)
  # phi_k <- c(0, 3.6/sqrt(N)*mapply(function(z) sum(1/sqrt(1-replace(hk, N-1, 0)[1:z]^2)), 1:(N-1))) # slower
  gss <- t(polar2rect(rep(1, N), rbind(theta_k, phi_k)))
  gss[1,] <- colMeans(gss[c(2, 3, 5, 6, 7),])
  gss[N,] <- colMeans(gss[N-c(1, 2, 4, 5, 6),])
  return(gss)
}

xyz <- t(polar2rect(rep(1, nrow(rad)), t(rad)))
gss <- t(polar2rect(rep(1, N), rbind(theta_k, phi_k)))
cols <- replace(rep("red", N), c(1, N), "green")
plot3d(xyz)
spheres3d(gss, col=cols, radius=0.03)

convhulln(GSS())