ビンゴゲーム

ビンゴゲームに参加する機会があった。
早く上がって商品を頂いた記憶があまりないが、今回は商品をゲットできた。
ビンゴになる確率は厳密に計算できて、ググればいろいろ出てくる。参加人数を考えればどれくらい商品を用意すればいいかが最適化されるはず。
今回はベタにシミュレーションして、リーチになるまでのくじ引き回数もカウントした。
詳細にみるとなんか違うが面倒なのでやめた。

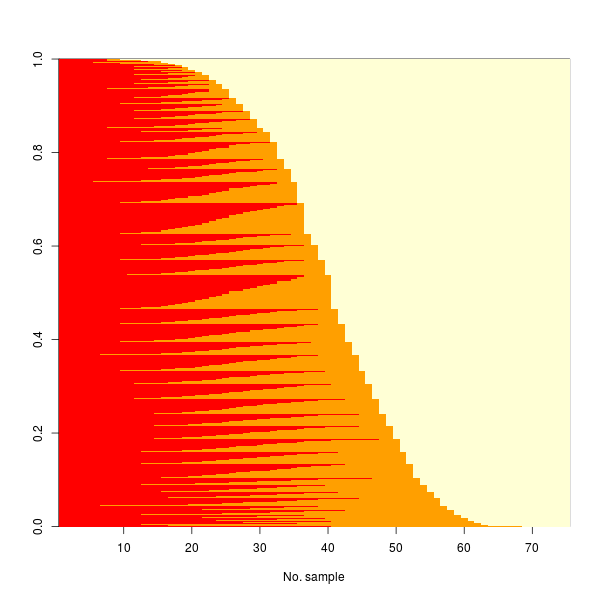
n_max <- 75    # 目の最大値
niter <- 10000 # シミュレーション回数
# ビンゴの紙を適当に作る。
# ビンゴの紙一枚は行列だが、演算のためベクトルにする。
mat <- replicate(niter, c(sapply(split(seq(n_max), rep(1:5, each=15)), sample, size=5)))
sheet <- matrix(0, 25, niter)
sheet[13, ] <- 1 # ビンゴの紙の真ん中は事前に空いている

s <- sample(n_max) # ビンゴのくじ引き
na <- rep(NA, 25)
# ビンゴのシート行列をベクトルとして扱うため、index を作成する。
g <- list(rep(1:5, 5), rep(1:5, each=5), replace(na, 5*(0:4)+1:5, 1), replace(na, 5*(0:4)+5:1, 1))
# リーチかビンゴかを判定する関数
f <- function(vec, p=5) any(mapply(function(x) any(tapply(vec, x, sum)==p), g))

res <- matrix(0, length(s), niter)
for(i in seq(s)){
	sheet[mat==s[i]] <- 1
	res[i, which(apply(sheet, 2, f, p=4))] <- 1 # リーチなら 1
	res[i, which(apply(sheet, 2, f, p=5))] <- 2 # ビンゴなら 2
}

bingo <- apply(res, 2, table)
res <- res[,order(bingo[3,])]
image(x=seq(n_max), z=res, xlab="No. sample")

赤は非リーチ、オレンジはリーチ、淡いのはビンゴ状態。