老化

ちょっと前に老化について話を聞いた。
そもそも、老化の定義とはなんだ、という話から始まって、「時間経過に伴う生体活動性の低下」とかなんやかんやあるらしいけど、その人は「死亡確率の上昇」と言っていた(エイジング)。
　
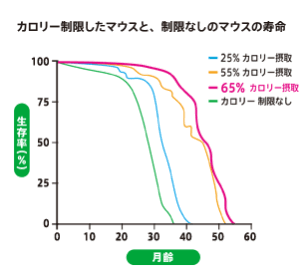
よく、カロリー制限するとマウスの寿命が伸びたとかいってこんな図が出る(けど、サルではそうはいかなかったとかいう報告も)。
Nature 489, 318–321 (13 September 2012) doi:10.1038/nature11432

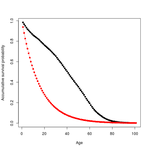
これは、年齢が低いと生存率が高く(死亡率が低い)、年齢が高いと生存率が低く(死亡率が高い)なるという、観察的にも直感的にも人生経験的にも合うことである。
それで、その人は、各年齢での死亡率が一定だとすると、生存曲線は下に凸の指数関数になる、と言っていた。
　
この話はここで忘れていたのだが、勉強会で生存曲線を描いたり、2011年度の人口動態統計というものを見つけたりしたので、やる気を出してシミュレーションしてみる。
　
年齢：
死亡率：
とすると、ある年齢までに生きている確率は

である。
今、年齢に応じて死亡率が高くなる現実モデルと、年齢に関係なく死亡率が一定の仮想モデルを考えると、
：
：
という感じにして、人口動態統計p22の性・年齢階級別震災死亡数（被災３県・その他別）の数値を利用する。
なので、これは実際の死亡率ではないです。

#適当に100歳くらいまでシミュレーション
age <- 0:100

#年齢階級ごとに死亡率が異なる場合
#これは地震の死亡数から算出したものなので実際とは異なる
#5歳ごとに階級が設定されているので、1歳ごとに戻す
d1 <- c(1.7, 1.3, 1, 1.4, 1.3, 1.7, 2.3, 2.8, 3.3, 3.6, 4.9, 6.9, 9.2, 9.4, 11.7, 12.2, 10.9)
d1 <- rep(d1, each=5)
d1 <- c(d1, rep(max(d1), length(age)-length(d1)))
#年齢によって死亡率が変わらない場合
#上の値の平均値が、ある年齢での1年間の死亡率にする
d2 <- rep(mean(d1), length(age))

d <- cbind(d1, d2)/100
#ある年齢までに生きている確率
S <- apply(1-d, 2, cumprod)

matplot(S, type="o", pch=16, xlab="Age", ylab="Accumulative survival probability")

年齢死亡率が一定ならそんな感じになった。
年齢死亡率の設定がちょっとだめだろう…ということで、いい値があればやり直そう。