
SKATという手法があるらしい。
kernel methodというなんとも中二病的ネーミングの手法を用いて、レアバリアントがどうたらこうたら言っていたがちょっと追いつけなかった。
SKATをやってみる。
昔やったロジスティック回帰をやると
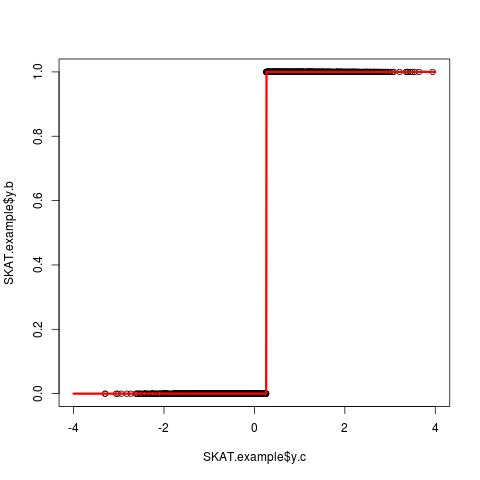
library(SKAT) data(SKAT.example) attach(SKAT.example) g0 <- glm(y.b ~ y.c, data=SKAT.example, family="binomial") p <- function(x){ 1/(1+exp(-sum(g0$coefficients * c(1, x)))) } s0 <- seq(-4, 4, length=1000) plot(SKAT.example$y.c, SKAT.example$y.b, xlim=range(s0)) points(s0, mapply(p, s0), type="l", col=2, lwd=3)
閾値を決めて表現型が決められているようだ。
# Compute the P-value of SKAT with default Beta(1,25) Weights # - without covariates # continuous trait obj <- SKAT_Null_Model(y.c ~ 1, out_type="C") SKATc0 <- SKAT(Z, obj) # dichotomous trait obj <- SKAT_Null_Model(y.b ~ 1, out_type="D") SKATd1 <- SKAT(Z, obj) # Compute the P-value of SKAT with default Beta(1,25) Weights # - with covariates # continuous trait obj <- SKAT_Null_Model(y.c ~ X, out_type="C") SKATc1 <- SKAT(Z, obj) obj.b <- SKAT_Null_Model(y.b ~ X, out_type="D") SKATd1 <- SKAT(Z, obj.b) # Compute the P-value of SKAT with default Beta(1,25) Weights # - Optimal Test SKAT2 <- SKAT(Z, obj, method="optimal.adj") SKAT3 <- SKAT(Z, obj.b, method="optimal.adj") # Compute the P-value of SKAT with Beta(1,30) Weights SKAT3 <- SKAT(Z, obj, weights.beta=c(1,30))