inheritance vector - 驚異のアニヲタ社会復帰の予備

読んだ。Am J Hum Genet. 1996 Jun; 58(6): 1323–1337.
　
inheritance vector というものがよくわからなかったのでLander-Green algorithm とともにいくつか検索。inheritance vector と何も考えずに検索するとプログラミングのinheritance が引っかかる。
Parametric and nonparametric linkage analysis: a unified multipoint approach.
http://csg.sph.umich.edu/abecasis/class/666.20.pdf
http://www.stat.berkeley.edu/~terry/Classes/s260.1998/Week8a/week8a/node13.html
Handling Marker-Marker Linkage Disequilibrium: Pedigree Analysis with Clustered Markers - ScienceDirect

http://lifesciencedb.mext.go.jp/result/analysis_technology.pdf
ランダー・グリーンアルゴリズム（１） - aggren0xの日記
 ランダー・グリーン・アルゴリズム（６） - aggren0xの日記
 2013-04-09 - aggren0xの日記

遺伝統計学の基礎―Rによる遺伝因子解析・遺伝子機能解析―

作者: 山田亮
出版社/メーカー: オーム社
発売日: 2010/09/04
メディア: 単行本（ソフトカバー）
購入: 7人クリック: 155回
この商品を含むブログ (38件) を見る

　
inheritance vector とは、家系内のある人の染色体が父親由来なのか母親由来なのかを $\{0,1\}$ のバイナリで記述したベクトル。
まず、家系内で父母が確定していない人をfounder と呼ぶ。ヒトで言えば、founder が $f$ 人いるとき、アレルは $2f$ 個ある。
家系内で父母が確定している人は、逆にnon-founder と呼ぶ。non-founder たちのアレルは、すべてfounder から由来している。inheritance vector はnon-founder が $n$ 人いるとき、長さ $2n$ のベクトルである。 $i$ 番目の人について、家系図を左から右、上から下へ昇順に並べて記述したとき、
$v=\{p_1,m_1,\dots,p_i,m_i,\dots,p_n,m_n\}$
と定義される。
　
ネットで拾った画像で詳細を追ってみる。この家系図と遺伝子型は論文と同じである。
やりたいことは、あるlocus $l$ のinheritance vector $v_l$ があるときに、あるlocus のマーカー $m_l$ を得る確率 $Pr(m_l|v_l)$ を求めることである。

　
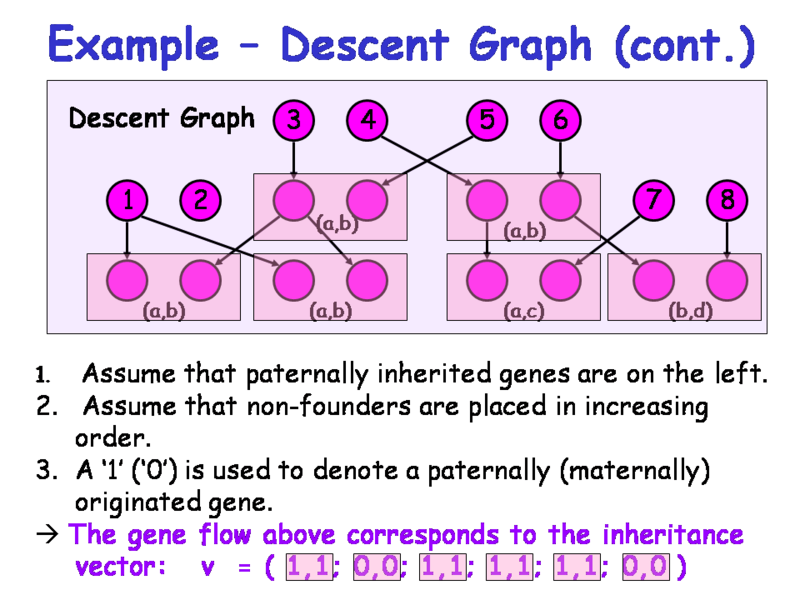
これをdescent graph として記述する。descent graph は人ノードを2つのアレルに分解して、父方アレルと母方アレルの伝わり方でエッジを引いたものである。慣例的に左が父方由来、右が母方由来で書かれることが多い。

　
いま、親が不明のfounder は1-8番のノードの染色体で示される。これは、もともとF0世代の父母と、F1 世代の婿(11)と嫁(14)に相当する。
ここで、各アレルの伝わり方が矢印ですべてわかっているとすると、inheritance vector は、家系図を左から右、上から下の昇順にみていって、親が既知であるnon-founder の (12), (13), (21), (22), (23), (24)さんたちの各アレルについて
$v=(1,1;0,0;1,1;1,1;1,1;0,0)$
となる。この場合は、1が父方由来、0が母方由来、としている。

　
descent graph から、founder graph を作る。例えばF0 の(1) が持っている3番のアレルは、F1 の(12)に遺伝して、F2 の(22)に遺伝している。F1 の(11)が持っている1番のアレルは、F2 の(21)に遺伝している。アレル単位でみるとバラけているが、2つの染色体をもつとヒトになることを意識すれば、1番のアレルと3番のアレルにはエッジがある、と考えられる。これをfounder graph という。
founder graph のエッジは、「アレルのgenotype」で、エッジは「ヒトのdiplotype genotype」である。
エッジで結ばれないノードは、singleton と呼ばれ、ぼっちである。

　
ノード(アレル)のgenotype が決まって欲しい。これは、エッジがヒトに対応していることを考えると、エッジで結ばれているノードが取りうるgenotype の組み合わせから解く。例えば、F2 の(21)は(a,b) であり、1番のアレルと3番のアレルがどちらも{a,b}のどちらかを取りうるとき、1番アレルと3番アレルは一意には決まらない。一方で、6番のアレルはF1 の(13)とF2 の(24) に受け継がれるが、(13)が(a,b)、(24)が(b,d) であることを考慮すると、積集合をとって6番のアレルは{b} に一意に決まる。

各アレルの取りうるgenotype を決めていくが、とりあえず適当にノードを選び、ありえそうなgenotype パターンで埋めてみて、埋まるようならば記録して、全体がうまく決まらないようならばその埋め方は破棄する。
　
founder graph のパターンが全部で $m$ 個、 $C_m$ とすると、アレルの割り当てパターンが $A_m$ となる。 $A_m$ は、singleton でなければ0か1か2個である。
graph component が例えば{1,3,5} のとき、アレルの割り当て確率は $Pr(a)^2Pr(b)+Pr(a)Pr(b)^2$ となる。
$A_m$ のなかのどれか $A_i$ が空集合のときは、 $Pr(m|v)=0$ である。また、singleton は確率1になるので、掛けても関係ないから無視してよい。
$Pr(a_{hi})=\prod_{{j:j\in C_i}}Pr(a_j)$ ： $a_{hi}$ は $A_i$ の要素で、 $C_i$ のグラフのノードにアレルが割り当てられた情報をもつベクトル。
$Pr(C_i)=\sum_{h:a_{hi}\in A_i}}Pr(a_{hi})$
$Pr(m|v)=\prod_{i=1}^m Pr(C_i)$

　
$v$ は $\{0,1\}$ のベクトルで、いろんな遺伝子座で長い行列を作ることができる。隣同士を比べて変化があればそこは組み換えがあったと考えてよく、隣り合うものを比較するときにマルコフ過程を使う、というのがキモらしい。