iCluster: オミックスデータの統合 - 驚異のアニヲタ社会復帰の予備

MikuHatsune2016-11-12

読んだ。
Bioinformatics(2009)25(22):2906-2912.
　
コピーナンバー(CNV)、発現データ(mRNA)、メチル化などのオミックスデータで、症例数 $n$ に対してパラメータ数 $p$ のデータ行列が複数ある。
各々の実験を勝手にやるのは、それはそれでいいが、CNV、発現、メチル化、プロテオームetc と $m$ 種類のいろいろなデータを取ったら、統合して考えたいと思うのは自然な発想である。
ここで、 $p\times n$ 次元のデータ行列 $X_m$ が、適当な係数行列 $W_m$ 、latent と呼ばれる、裏で共通して存在しているであろう(だが、観測はできない)因子 $Z$ と誤差 $\epsilon_m$ を用いて
$X_m=W_m Z +\epsilon_m$
として $Z$ を求めたい。
iCluster パッケージにある。
　
あるオミックス実験(gene exprssion とか)は $p\times n$ の行列データをヒートマップ化して、階層的クラスタリングで系統樹を書くことが多いが、 $m$ 個のオミックス実験で $n$ 症例たちがk-means で $k$ クラスターに分類できる、とする。
$X$ は平均で中央揃えした $p\times n$ 次元の行列である。 $X$ は $k$ 群でわけられ( $C$ )、クラスター平均ベクトル $\{m_1,\dots,m_k\}$ について郡内誤差を最小化する。
$min\sum_{k=1}^K \sum_{C(i)=k} ||x_i-m_k||^2$
　
$Z=(z_1, \dots, z_k)$ となる行列を作るが、ここで $n_k$ は $k$ 番目のクラスター内のサンプル数で、
$z_k^{'}=(0,\dots,0,\frac{1}{\sqrt{n_k}},\dots,\frac{1}{\sqrt{n_k}},0,\dots,0)^{'}$
であり、 $\frac{1}{\sqrt{n_k}}$ の部分は $n_k$ 個ある。また、 $\sum_{k=1}^{K}n_k=n$ である。
　
$X^{'}X$ をグラム行列( $G=(v_1,\dots,v_n)$ のとき、内積[tex:G_{ij}=] で定義される)とすると、k-means で郡内誤差は
$trace(X^{'}X)-trace(ZX^{'}XZ^{'})$
と表されるらしく、前者はtotal variance, 後者はbetween-cluster varianvce となるので、後者を最大化すれば全体の最小化が達成される。
$Z$ は連続量でもいいので、 $K$ 個の降順のeigenvalue で $\hat{Z}^{*}=E=(e_1,\dots,e_K)^{'}$ とできる。
　
大事なのはGaussian latent variable である $Z$ で $X$ を分解する。
$X=WZ+\epsilon$
$X$ はデータ行列で $p\times n$ 、 $W$ は係数行列で $p\times (K-1)$ 、 $Z$ はlatent variable で $(K-1)\times p$ 、 $\epsilon$ は対角成分が共分散の行列で $p\times p$ である。
EM アルゴリズムでなんやかんやしてたら解ける。また、 $p>>n$ 問題のときにスパースに解くことができるし、LASSO による係数選択も行う。
$\lambda$ が大きくなってスパースになると、 $W$ の多くが0 になる。 $W$ は係数行列なので、遺伝子発現やCNV など各遺伝子（ $p$ なのでこれはたいていすごい大きな数である）の作用の強さを決めている。大きい $\lambda$ になるとほとんどが0 になり、本当に作用の強い遺伝子( $p$ )しか残らなくなるので、解釈は楽になる。
iClusterPlus
　
適切なk-means クラスターの数はproportion of deeviance (POD) という統計量で測ることができ、shrinkage parameter $\lambda$ のときのPOD が最小化のときが最もよさそうなクラスターの分け方になる。論文では $k=4$ である。

par(mfrow=c(1, 2))
for(i in 1:2){
  heatmap.2(t(breast.chr17[[i]]), trace="none", col=gplots::greenred(100), scale="row", hclustfun=function(x) hclust(x, method="ward.D2"))
}

CNV. Fig2A に相当する。

　
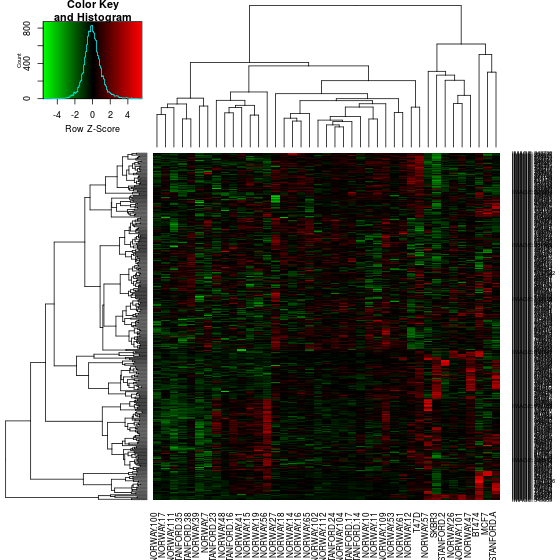
gene expression. Fig2A に相当する。

　

library(iCluster)
data(breast.chr17)
fit <- mapply(function(k) iCluster(breast.chr17, k=k, lambda=c(0.2,0.2)), 2:5, SIMPLIFY=FALSE)
par(mfrow=c(2, 2))
for(i in seq(fit)) plotiCluster(fit=fit[[i]], label=rownames(breast.chr17[[2]]))
pod <- mapply(compute.pod, fit)

症例間の相関。Fig2B に相当する。

　

plotHeatmap(fit[[which.min(pod)]], datasets=breast.chr17)

k クラスターに分けたあとの、 $m$ 個の実験のクラスタリング。行はパラメータ $p$ , 列が症例 $n$ に対応している。

　
こうして新規に分けられたkクラスターで、生存曲線を書いて差があると、オミックス統合した解析がいいでしょう、となる。
論文では、乳癌のHER/ERBB, 肺癌のEGFR などをメルクマールに解析している。