ある2群の比較で、介入群の前後比較では有意で、非介入群の前後比較では有意でなかったときに、このふたつの結果を比較して「介入群で有意に改善が認められた」と結論づけるのがダメなのはどうしてですか

という質問を受けた。
http://www.bmj.com/content/342/bmj.d561.long
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3286439/
　
設定としては、n=30 人ずつの2群に対して,片方にはアンチエイジング効果がありそうな薬、対照にはプラセボを与えて、投与時(t=0)と6ヶ月後(t=6)に効果をそれぞれ測定する。
介入群では、t=0 とt=6 との比較で有意であり、対照ではt=0 とt=6 との比較で有意ではなかった。これらの結果をもって、「介入群の薬は、有意に効果があった」と結論づけている。
　
これがダメなのはどうしてだろうか。
　
帰無仮説検定の枠組みから考えれば、上記の解析で行われたのは、「介入群でt=0 とt=6 の比較」と「対照群でt=0 とt=6 との比較」であり、「介入群と対照群の比較」は行われていないことに注意しなければならない。いやいや、「介入群のp値」と「対照群のp値」の比較をもって、「介入群と対照群の比較」が行われているでしょう、と思う方もいるかもしれないが、「介入群と対照群の帰無仮説検定」は行われていないことに注意しなければならない。
　
この研究で本当に比較すべきだったのは、「介入群でのスコアの改善具合と、対照群でのスコアの改善具合」の比較だった。
また、統計とかバイオインフォマティクス的に言えば、「 $\alpha$ エラーが制御されない」からだと思う。
　
というのが理論的な枠組みだが、もうちょっとわかりやすくならないかと聞かれたので、シミュレーションをしてみる。
　
「 $\alpha$ エラーが制御されない」状況を示すため、帰無仮説が真という、本当は神様しか知らない状況をシミュレーションで作り出す。状況設定としては、A群とB群のふたつにそれぞれ30人患者が含まれ、t=0 では平均0、標準偏差2 の正規分布から両群ともにランダムにデータを作る。
t=6 では、平均0.5、標準偏差1 の正規分布に従う増加量(統計学的には効果量 effect size) が加算される、とする。
この設定では、n=30 人は両群ともに、t=0 とt=6 で対応があるので、t=0 とt=6 での比較は、各群(within group) で対応のあるt検定をする。シミュレーションでは10000回行う予定なので、p値は20000個出る。

# 論文上の設定
n <- 30
g <- rep(1:2, each=n)
sd1 <- 2
niter <- 10000
alpha <- 0.05
f <- function(m=0){
  baseline <- rnorm(n*2, 0, sd1)
  increase <- rnorm(n*2, m, 1)
  final <- baseline + increase
  paired <- final - baseline
  p1 <- mapply(function(z) t.test(z, var.equal=TRUE)$p.value, tapply(paired, g, c))
  p3 <- t.test(paired ~ g, var.equal=TRUE)$p.value
  return(c(p1, p3))
}

p <- replicate(niter, f(m=0.5))
mean(p[3,] < alpha)     # 介入群と対照群が有意に異なる確率
mean(p[1:2,] < alpha)   # 介入群の前後比較と、対照群の前後比較がそれぞれ有意になる確率
sig <- p[1:2,] < alpha
table(sig[1,], sig[2,]) # 介入群の前後比較で有意になる場合と、対照群の前後比較で有意になるパターン分け

　
いま、帰無仮説が真であることが分かっているので、考えるべきことは、帰無仮説が真のときに棄却する確率、つまりtype I error のalpha である。A群とB群の検定をそれぞれ行うとき、「A群のなかのA1 とA2 には差が(母集団を見ればまったく、本当に)ないにも関わらず、母集団からランダムサンプルされた標本については検定的には有意になる」確率がalpha(=0.05) である。
これはシミュレーションで簡単に分かる。

mean(replicate(3000, t.test(rnorm(1000), rnorm(1000))$p.value) < 0.05)

このコードは、仮説検定をするふたつの標本集団について、(神様だけが知っている)母集団として平均0、標準偏差1 の正規分布を仮定している。帰無仮説検定は、みんなが実験して得た手元のデータ(標本集団)に差があることを言いたいのではなく、その手元のデータが生じた母集団が異なるかどうかを、そんなことは神様しか知らないので手持ちのデータからどうにか言おう、という試みである。
まったく同じ正規分布から、1000と1000の標本集団を取り出して、t検定をしてp値を計算して、p値が0.05以下の数(割合)を計算すると、0.05 くらいになる。0.05ではなく $\alpha$ にすると、結果は $\alpha$ に近くなる。
　
さて、A群とB群でそれぞれ仮説検定をしたとき、有意か非有意かで2*2 通りの結果になる。「帰無仮説が真」という状況が続いたままで、つまり確率p( $\alpha$ でもいいけど)で有意になることが分かっているので、

.	Aが有意	Aが非有意
Bが有意	$pp$	$p(1-p)$
Bが非有意	$p(1-p)$	$(1-p)(1-p)$

(ただし、AとBの仮説検定は独立であると仮定している)
　
多重検定的な話になるが、「A群では有意で、B群では有意でなかった」(その逆もあり)の確率は、 $2p(1-p)$ になるので、 $0 < p < 0.5$ ではtype I error として決めたp ( $\alpha$ でもいいけど) より大きくなる。このため、有意になる、という結果を導きやすくなるのだが、これはダメである。普通は、こういうときはtype I error が最終的に $\alpha$ と同等か $\alpha$ 以下になるように、ボンフェローニ的に割ったりいじったりするのである。
　
さて、次に考えるのは、「A群の前後比較では差があることがわかっていて、B群の前後比較も差があることが分かっているときに、A群の検定結果とB群の検定結果を比較する」ことである。これは、前述の内容が「帰無仮説が真」、つまり差がないことが神様は知っていて我々も知っているときにtype I error $\alpha$ で有意になってしまうことに対して、「差がある」(効果量 effect size という)ということが前提として分かっているのに、「差がないという帰無仮説を真」として仮説検定をするのは、どう考えても日本語がおかしいのだが、帰無仮説検定の枠組みはそうなのでそうしてしまう。ただし、「差がないという帰無仮説が真」という前提で有意差が出る、という結果になる確率が $\alpha$ であり、どう考えても $\alpha$ より有意になりやすいので、その確率が検出力 power というものである。これは「差が本当にあるのに、差がないと間違えてしまう」type II error $\beta$ に対応して、 $1-\beta$ と定義されている。

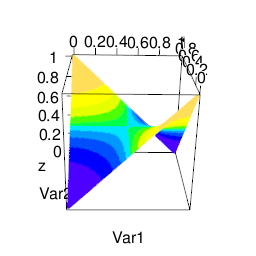
これについて、上の2*2表を使うと、A群の検出力が $p_A$ 、B群の検出力が $p_B$ であるときに、「片方が有意で片方が非有意」になる確率は、 $p_A(1-p_B)+(1-p_A)p_B$ になる。これは簡単に表現できて、片方が検出力1、片方が0 のときに最大となる。

p <- seq(0, 1, by=0.01)
pp <- expand.grid(p, p)
z <- pp[,1]*(1-pp[,2]) + pp[,2]*(1-pp[,1])
qu <- quantile(z, seq(0, 1, by=0.1))
i <- cut(z, qu, include.lowest=TRUE)
rgl::plot3d(cbind(pp, z), col=topo.colors(length(qu))[i])

論文のシミュレーションでは、介入群の前後比較も、対照群の前後比較も検出力0.75 になるので、「片方が有意で片方が非有意」の確率は0.375 になる。

長々書いて全体の整合性がややあやしくなってきたけど、結局、type I error が制御されないのが原因と思う。