markdown 形式のrmarkdown とknitr を使って、授業資料の作成および解析結果の報告、宿題の提出などやっている。
HTML にすることでrgl の3D プロットなども出せるので、3D データを扱っているときにもよさげ。
真面目にやるならpandoc をインストールしてrender して…というので初心者は挫折する可能性があるが、Rstudio ならばknitr ボタンをポチるだけでできる。
いくつかハマった箇所。
いい感じの見出しや目次をつけたいとき、一番上に書いておけばいい感じになる。
---
title: "Title"
author: "Author name"
date: "Any date such as created or presented date"
output:
html_document:
toc: true
toc_depth: 4
number_section: true
---
Created at `r Sys.time()`.
rmarkdownのchunk オプションをまとめて書いておけば一括で変更できる。
```{r echo=FALSE, warning=FALSE, message=FALSE, comment=""}
knitr::opts_chunk$set(echo=TRUE, eval=FALSE, warning=FALSE, message=FALSE, comment="")
```
本文自体はmarkdown 記法にしたがってかく。例えば見出しにリンク付きハイライトを書いたとしても、目次では目次番号がHTML 内リンク、見出し文字がリンク先へリンク、となっている。
rgl は少し挙動がオカシイときがある。こちらを参考にオプションをセットし
```{r setup, eval=TRUE, echo=FALSE}
library(rgl)
knitr::knit_hooks$set(rgl = hook_webgl)
```
実際にplot3d を出力する部分はrgl=TRUE を設定すればよい。
```{r rgl=TRUE, eval=TRUE}
plot3d()
```
しかし、ubuntu が悪いのかrgl するデータ容量が大きすぎるのが悪いのか、chrome が悪いのか、結構な頻度で
You must enable Javascript to view this page properly.
と言われてhtml 上、表示されないことがある。windows に持っていくと見れることもある。
というわけでサンプル。.Rmd として保存して、render するかRstudio でknitr ボタンをポチる。
---
title: "Matrix and Gram-Schmidt orthonormalization process"
author: "@Med_KU"
date: "20160705"
output:
html_document:
toc: true
toc_depth: 4
number_section: true
---
Created at `r Sys.time()`.
```{r echo=FALSE, warning=FALSE, message=FALSE, comment=""}
knitr::opts_chunk$set(echo=TRUE, eval=FALSE, warning=FALSE, message=FALSE, comment="")
```
```{r setup, eval=TRUE, echo=FALSE}
library(rgl)
knitr::knit_hooks$set(rgl = hook_webgl)
```
Vector is mathematically a set of [scalar](https://en.wikipedia.org/wiki/Scalar_(mathematics)). Vector has scalar values and direction.
R keeps data by *vector* structure. This is an essential form. This is defined by `c`.
The data made in R is called *object*.
```{r}
dat <- c(1, 2, 10, 5, 9, 291)
dat
```
You can access to i th element in the *vactor* by `dat[i]`.
```{r}
dat[4]
```
You can modify the *vector object* by adding or reducing its elemetns.
```{r}
c(dat, 4, 1, 5, 12312)
dat[-4]
```
You can sum/diff/multiply/divide the *vector* or each element between *vector*s.
```{r}
# define another vector
dat1 <- c(3, 13, 64, 11, 0, 4)
sum(dat)
dat[3] + dat[1]
dat + dat1
dat[1] - dat[2]
diff(dat)
dat - dat1
dat[1] * dat[5]
prod(dat)
dat * dat1
dat/dat1
```
*Matrix* is a 2 dimensional data structure. *Matrix* keeps data as N length vectors by M columns.
This is called N by M (dimension) *matrix*. *Matrix object* is defined by `matrix`.
```{r}
mat <- matrix(dat, nr=2, nc=3)
mat
```
We can access the cell (or element) in the matrix by indicating indices. If you want to take the cell of second row and third column, write `mat[2, 3]`.
```{r eval=TRUE, echo=FALSE}
hoge <- matrix(c("", "", "↓", "→", "→", "i, j"), nr=2, byrow=TRUE)
```
```{r eval=TRUE, echo=TRUE, comment=""}
hoge
```
**Warning!!** Elements in a matrix object should be the same class. In upper case, "", arrows, and 'i, j' are *character*. If there are various type of objects, object type will be forced to transform into *complex* > *character* > *float* > *integer* automatically. To avoid this problem, *data.frame* is sometime used.
Arithmetic operators for *matrix* are two ways. One is an operator for each element. Like arithmetic operators for *vector* in upper cases, simple description of `+`, `-`, `*`, and `/` return results of each element.
That is, there are two matrices $A=\begin{pmatrix}a_{1,1}&a_{1,2}\\a_{2,1}&a_{2,2}\end{pmatrix}$ and $B=\begin{pmatrix}b_{1,1}&b_{1,2}\\b_{2,1}&b_{2,2}\end{pmatrix}$, `+` operator returns $A+B=\begin{pmatrix}a_{1,1}+b_{1,1}&a_{1,2}+b_{1,2}\\a_{2,1}+b_{2,1}&a_{2,2}+b_{2,2}\end{pmatrix}$
```{r echo=FALSE}
mat1 <- matrix(1:4, nr=2)
mat2 <- matrix(5:8, nr=2)
```
```{r}
mat1 + mat2
mat1 * mat2
```
On the other hand, `%*%` operator returns matrix mutiplication $AB=\begin{pmatrix}a_{1,1}b_{1,1}+a_{1,2}b_{2,1}&a_{1,1}b_{1,2}+a_{1,2}b_{2,2}\\a_{2,1}b_{1,1}+a_{2,2}b_{2,1}&a_{2,1}b_{1,2}+a_{2,2}b_{2,2}\end{pmatrix}$.
**Optional**: `%*%` operator for *vector* returns inner product.
Gram-Schmidt process is a method to orthonormalize a set of vectors in an inner product space. We generally suppose 3 dimensional space ($\mathbb{R}^3$) but it can be generalized in $\mathbb{R}^n$ space.
You replace a set of basis $\boldsymbol{v}=\{v_1, v_2, v_3\}$ with another set of basis $\boldsymbol{u}=\{u_1, u_2, u_3\}$. During the process, *normalization* and *orthogonalization* can be done.
Given *vector*s $\boldsymbol{x}$ and $\boldsymbol{y}$, these processes are performed as below.
***normalization***: *Normarization* means set length of *vector* (*norm*) 1. Length is difined as $|\boldsymbol{x}|$. That is, *normalization* returns $\boldsymbol{x}=\cfrac{\boldsymbol{x}}{|\boldsymbol{a}|}$.
***orthogonalization***: *Orthoganal* means crossing two *vector*s by 90 degree. Angle between *vector*s $\boldsymbol{x}$ and $\boldsymbol{y}$ is difined as $\theta$, and $\theta$ can be also defined by *inner product*
$cos{\theta}=\cfrac{\boldsymbol{x}\cdot \boldsymbol{y}}{|\boldsymbol{x}||\boldsymbol{y}|}$.
When $\theta=\pi$, $cos{\theta}=0$. That is $\boldsymbol{x}\cdot \boldsymbol{y}=0$.
Let's take a *vector* $\boldsymbol{a}$. This *vector* has three *vector*s `a1 <- c(1, 1, 1)`, `a2 <- c(1, -1, 2)`, and `a3 <- c(-1, 1, 3)` in itself. Data structure looks like *matrix*.
```{r eval=TRUE}
a <- cbind(c(1, 1, 1), c(1, -1, 2), c(-1, 1, 3))
```
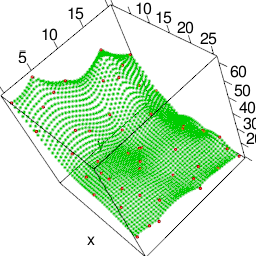
```{r eval=TRUE, out.width=480, out.height=480, fig.width=7, fig.height=7}
# install.packages("scatterplot3d")
s <- scatterplot3d::scatterplot3d(t(cbind(0, a)), pch=16, xlab="x", ylab="y", zlab="z")
dt <- seq(0, 1, length=100)
for(i in seq(ncol(a))){
s$points3d(t(outer(a[, i], dt)), cex=0.01, col=i+1)
}
```
```{r rgl=TRUE, eval=TRUE}
plot3d(t(cbind(0, a)), pch=16, xlab="x", ylab="y", zlab="z")
spheres3d(t(a), radius=0.05)
for(i in seq(ncol(a))){
lines3d(rbind(0, a[, i]), lwd=2, col=i+1)
}
```
From *vector*s $a$, you want to get Gram-Schmidt *vector*s $u$. Gram-Schmidt process is performed as below.
1. STEP 1: $u_{1}=\cfrac{a_{1}}{|a_{1}|}$
2. STEP 2: $b_{2}=a_{2}-(a_{2}\cdot u_{1})u_{1}$, then $u_{2}=\cfrac{b_{2}}{|b_{2}|}$
3. STEP 3: $b_{3}=a_{3}-(a_{3}\cdot u_{1})u_{1}-(a_{3}\cdot u_{2})u_{2}$, then $u_{3}=\cfrac{b_{3}}{|b_{3}|}$
$b$ is a temporal objects.
Gram-Schmidt process is much major and famous algorithm. Someone has already implemented in R as a function.
[pracma](https://cran.r-project.org/web/packages/pracma/index.html) package has a function `gramSchmidt` to perform it. A precise result is $u_{1}=\cfrac{1}{\sqrt{3}}(1, 1, 1)$, $u_{2}=\cfrac{1}{\sqrt{42}}(1, -5, 4)$, and $u_{3}=\cfrac{1}{\sqrt{14}}(-3, 1, 2)$.
```{r echo=TRUE, eval=TRUE}
# install.packages("pracma")
library(pracma)
(a_g <- pracma::gramSchmidt(a))
```
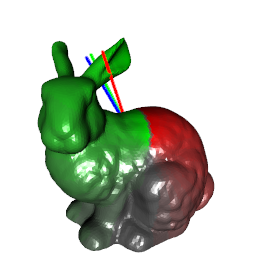
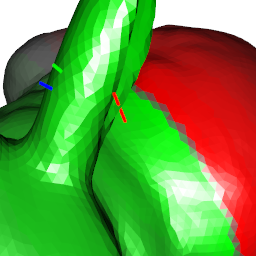
```{r rgl=TRUE, eval=TRUE}
plot3d(t(cbind(0, a)), pch=16, xlab="x", ylab="y", zlab="z")
spheres3d(t(a), radius=0.05)
for(i in seq(ncol(a))){
lines3d(rbind(0, a[, i]), lwd=2, col=i+1, lty=3)
}
spheres3d(t(a_g$Q), radius=0.05, col="yellow")
for(i in seq(ncol(a_g$Q))){
lines3d(rbind(0, a_g$Q[, i]), cex=0.01, lwd=4, col=i+1)
}
```
1. Define any *vector* as you like.
2. Calculate mean of that *vector* by writing down the difinition of mean and using pre-implemented function in R.
3. Define 3 by 3 *matrix* $M$ as you like.
4. Calculate *matrix multiplication* $M^3$.
5. Perform Gram-Schmidt process of $M$. As shown in above, you need 3 steps.
6. Check whether STEP 5 is performed successfully, that is, compute *inner product* of the basis of Gram-Schmidt $M$ and length of it (This procedure needs multiplication and summation. These functions are in R.).
