3次元空間の補間 kriging

3次元空間の補間 interpolation をしたい。
空間統計学やGIS ではkriging と呼ばれる手法を用いている。
interpolation 自体はakima, kriging はpracma, kriging パッケージでできる。
pracma のkriging は、補間して推定したい点をひとつ入れれば、それに対応するZ軸の値を返す仕様で、kriging のkriging はある範囲のすべての補間推定値を返す仕様っぽい。


　
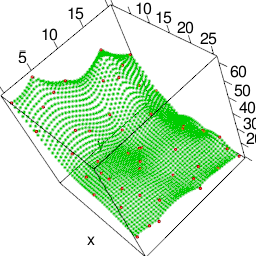
本当はこれくらい複雑なデータにやりたいけれども、うまく補間幅を選ばないとデータ容量で爆発する。

library(akima)
library(rgl)
data(akima)
# data
rgl.spheres(akima$x,akima$z , akima$y,0.5,color="red")
rgl.bbox()
# bivariate linear interpolation
# interp:
akima.li <- interp(akima$x, akima$y, akima$z,
                   xo=seq(min(akima$x), max(akima$x), length = 100),
                   yo=seq(min(akima$y), max(akima$y), length = 100))
# interp surface:
rgl.surface(akima.li$x,akima.li$y,akima.li$z,color="green",alpha=c(0.5))
# interpp:
akima.p <- interpp(akima$x, akima$y, akima$z,
                   runif(200,min(akima$x),max(akima$x)),
                   runif(200,min(akima$y),max(akima$y)))
# interpp points:
rgl.points(akima.p$x,akima.p$z , akima.p$y,size=4,color="yellow")
# bivariate spline interpolation
# data
rgl.spheres(akima$x,akima$z , akima$y,0.5,color="red")

library(pracma)
library(kriging)
# pracma package でやる
## Interpolate the Saddle Point function
f <- function(x) x[1]^2 - x[2]^2 # saddle point function
set.seed(8237)
n <- 36
x <- c(1, 1, -1, -1, runif(n-4, -1, 1)) # add four vertices
y <- c(1, -1, 1, -1, runif(n-4, -1, 1))
u <- cbind(x, y)
v <- numeric(n)
for (i in 1:n) v[i] <- f(c(x[i], y[i]))

xy <- c(0.3, 0.3)
pkr <- pracma::kriging(u, v, xy)
plot3d(cbind(u, v))
spheres3d(matrix(c(xy, pkr), nr=1), radius=0.05, col=2)

# kriging package のほうで同じことをやる
kkr <- kriging::kriging(akima$x, akima$y, akima$z, lags=10, pixels=50)
plot3d(kkr$map, col=3)
spheres3d(akima$x, akima$y, akima$z, radius=0.5, col=2)