Interrupted time-series analysis - 驚異のアニヲタ社会復帰の予備

MikuHatsune2015-09-22

Interrupted time-series analysisという解析法をやろうと思ったのでやってみたメモ。
J Clin Pharm Ther. 2002 Aug;27(4):299-309.(PDF)を読めばいい。
　
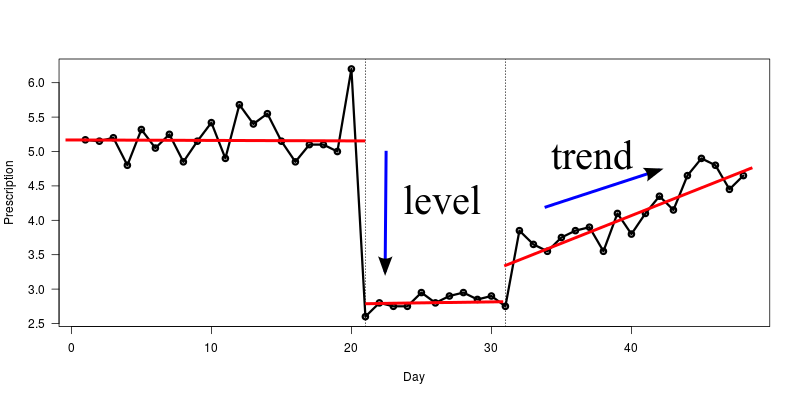
データとしては、次の図のような日時と処方数のデータについて、とあるイベントが起きたときのそのイベントの影響力というものを推定したい。
データはNew Hampshire の処方数データで、とある瞬間に処方数は3つまでにしてくださいね(ﾆｺｯという政策が始まった。これが左側の破線。
もうひとつは、処方は3つまでにしてください、という政策から変更して、1ドルのcopay がもらえる(?)という政策である。これが右側の破線。
　
ITS のモデルは、単純に level とtrend のふたつのパラメータの推定である。level は介入前後での程度の大きさ、trend は介入前後で増えるもしくは減る傾向があるかないか、である。これらを簡単に線形回帰で推定する。
$Y(t)=\beta_0+\beta_1T_1(t)+\beta_2I_1(t)+\beta_3U_1(t)$
$\beta_i$ ：推定するパラメータ
$T_j(t)$ ：観察開始時点からとある時刻 $t$ までの経過時間。これのパラメータ $\beta_1$ は、全体のtrend を示す。
$I_j(t)$ ：とある介入 $j$ があるかどうか。つまり、0 or 1である。これのパラメータ $\beta_2$ は、介入の効果の大きさ、つまりlevel である。
$U_j(t)$ ：とある介入 $j$ があってから、時刻 $t$ における経過時間。これのパラメータ $\beta_3$ は、介入 $j$ があってからのtrend である。
　
これをなんでもいいから最尤推定する。

m <- lm(prescription ~ observation + intervention1 + time1, data=subset(a, intervention2==0))

Call:
lm(formula = prescription ~ observation + intervention1 + time1, 
    data = subset(a, intervention2 == 0))

Coefficients:
  (Intercept)    observation  intervention1          time1  
    5.0481579      0.0158421     -2.6450000      0.0005215

なんかずれてる。まあ、基本的には5つくらいの処方があったけど、3つまで政策以降は $\beta_2=-2.65$ のlevel低下効果があって、このモデルオブジェクトをsummary してもらうと、p値が出る。

Call:
lm(formula = prescription ~ observation + intervention1 + time1, 
    data = subset(a, intervention2 == 0))

Residuals:
     Min       1Q   Median       3Q      Max 
-0.45163 -0.14318 -0.01727  0.10516  0.83500 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)    5.0481579  0.1249961  40.387  < 2e-16 ***
observation    0.0158421  0.0104345   1.518    0.141    
intervention1 -2.6450000  0.2091040 -12.649 7.36e-13 ***
time1          0.0005215  0.0276965   0.019    0.985    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2691 on 27 degrees of freedom
Multiple R-squared:  0.9544,	Adjusted R-squared:  0.9494 
F-statistic: 188.5 on 3 and 27 DF,  p-value: < 2.2e-16

　
ただし、ITS は時系列データであり、時系列データに自己相関がある場合には、標準誤差の過小評価と、介入による効果の過大評価が起きてしまい、有意なp値を報告しがちである。
そのようなときにDurbin–Watson testを使う。これは帰無仮説が自己相関なしとして検定する。
論文の例では自己相関調整後に検定したらp値が0.49 だったといっているがようわからん。が、このデータ自体には自己相関はなさげらしいからそのままITS を使うが、ks.testで有意じゃなかったからt.test します的なノリじゃないのかこれ…

library(car)
durbinWatsonTest(m, max.lag=4)

 lag Autocorrelation D-W Statistic p-value
   1     -0.20491267      2.392568   0.572
   2      0.08374096      1.812606   0.400
   3     -0.12169186      2.217753   0.576
   4     -0.33120901      2.582121   0.060

rstan で実装が簡単そうなモデルなのでいつかやる。

　

observation,prescription,month,intervention1,time1,intervention2,time2
1,5.17,1,0,0,0,0
2,5.15,2,0,0,0,0
3,5.2,3,0,0,0,0
4,4.8,4,0,0,0,0
5,5.32,5,0,0,0,0
6,5.05,6,0,0,0,0
7,5.25,7,0,0,0,0
8,4.85,8,0,0,0,0
9,5.15,9,0,0,0,0
10,5.42,10,0,0,0,0
11,4.9,11,0,0,0,0
12,5.68,12,0,0,0,0
13,5.4,13,0,0,0,0
14,5.55,14,0,0,0,0
15,5.15,15,0,0,0,0
16,4.85,16,0,0,0,0
17,5.1,17,0,0,0,0
18,5.1,18,0,0,0,0
19,5,19,0,0,0,0
20,6.2,20,0,0,0,0
21,2.6,21,1,1,0,0
22,2.8,22,1,2,0,0
23,2.75,23,1,3,0,0
24,2.75,24,1,4,0,0
25,2.95,25,1,5,0,0
26,2.8,26,1,6,0,0
27,2.9,27,1,7,0,0
28,2.95,28,1,8,0,0
29,2.85,29,1,9,0,0
30,2.9,30,1,10,0,0
31,2.75,31,1,11,0,0
32,3.85,32,1,12,1,1
33,3.65,33,1,13,1,2
34,3.55,34,1,14,1,3
35,3.75,35,1,15,1,4
36,3.85,36,1,16,1,5
37,3.9,37,1,17,1,6
38,3.55,38,1,18,1,7
39,4.1,39,1,19,1,8
40,3.8,40,1,20,1,9
41,4.1,41,1,21,1,10
42,4.35,42,1,22,1,11
43,4.15,43,1,23,1,12
44,4.65,44,1,24,1,13
45,4.9,45,1,25,1,14
46,4.8,46,1,26,1,15
47,4.45,47,1,27,1,16
48,4.65,48,1,28,1,17