ふたつの分布が違うのをどう示したらいいですか

こんな記事を書いたらごく狭い範囲で反響があった。
mikuhatsune.hatenadiary.com

ガンマ分布の記事感動しました。そんなガンマ分布マスターであられる驚異のアニヲタさんに質問するもの失礼なほど低級な質問なんですが、、、
ある疾患があって、その疾患発症間隔（病院で観察された日）の分布が院外と院内で違う、ということを言いたいようです。ブログの例の混合分布ではなく、すでに違う二つの群のデータが取れているとして、その群に差がある、と言いたいと。
この場合は指数分布というかガンマ分布で回帰して係数がちがうと言えばいいでのでしょうか?

と聞かれたので考えた。

群が分かれている、ということなので、分布を近似してその近似した分布を決定しているパラメータを比較するか、分布を近似せずにそのまま扱うリサンプリングな方法で考えればいいのではないだろうか。
データはシミュレーション用に再度、ガンマ分布から適当に生成されたとする。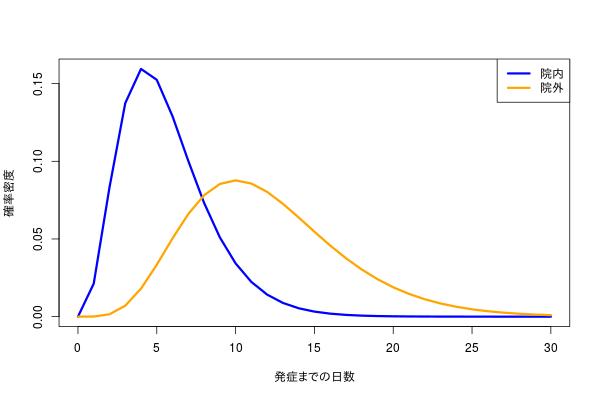

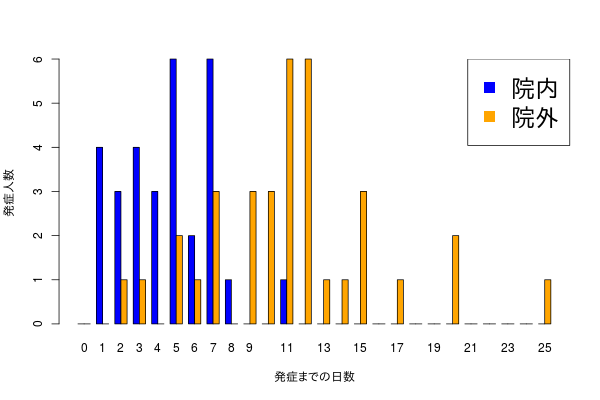
データを生成するガンマ分布

シミュレーションデータはこんな感じになる。30症例ずつくらいにしている。

シミュレーションデータ

リサンプリングでやってみる。
いま手元にあるデータから経験分布を作って、そのデータと同じ数だけ重複を許して、すなわちreplace=TRUE でいくつも偽データセットを作る。
その上で平均（分布が非対称ならmedian なり適当な要約量を使う）をとり、平均の差分が0なら一緒（みたいなもの）とみなし、差があれば違う、と考える。0をまたぐ偽セット数をp値っぽいものとみなす。
今回のシミュレーション結果としては

    2.5%      50%    97.5% 
4.842738 6.521429 8.466786 

となり、すべて平均の差が0以上なので、ふたつの分布は違うのだろう、と判断する。

stanでやってみる。
分布がなんらかのパラメータを持つ有名な分布で近似できるならば、そのパラメータを推定しにかかる。パラメータから平均など要約量が取れるので、それを比較する。

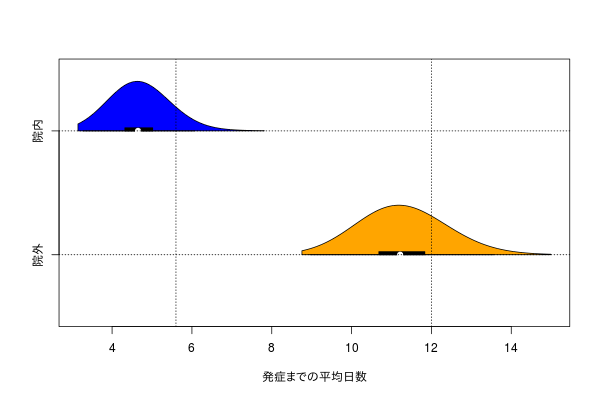
パラメータ推定値から計算した平均値の差は、リサンプリングでしたときとだいたい同じになる。これもふたつの分布は違うようだ、と判断する。

    2.5%      50%    97.5% 
4.704524 6.579990 8.594733 

検定的に考えるならこんな感じだが、分布の形を平均値というひとつの統計量にして、しかもその平均値が分布をよく表すとも言えないのにこれでなんとかするのはどうなんだろうかと思う。
少し前に別の人に聞かれて、分布の形があるならカルバックライブラーとかJensen-Shannon とかどう?って返答したことがあるが、これを使った検定はあるのだろうか（適当

shape <- c(4, 6)
scale <- c(1.4, 2)
x <- 0:30
lab <- c("院内", "院外")
n <- c(30, 35)

d <- t(mapply(dgamma, x, list(shape), scale=list(scale)))
cols <- c("blue", "orange")
matplot(x, d, type="l", lty=1, col=cols, lwd=3, xlab="発症までの日数", ylab="確率密度")
legend("topright", legend=lab, lty=1, col=cols, lwd=3)

dat <- lapply(mapply(rgamma, n, shape, scale=scale, SIMPLIFY=FALSE), floor)
day_max <- max(unlist(dat))
b <- sapply(lapply(dat, factor, 0:day_max), table)

barplot(t(b), beside=TRUE, col=cols, xlab="発症までの日数", ylab="発症人数")
legend("topright", legend=lab, pch=15, col=cols, cex=2)

alpha <- 0.05
# リサンプリング
niter <- 1000
diff_mean <- replicate(niter, diff(sapply(mapply(sample, dat, replace=TRUE), mean)))
hist(diff_mean, xlab="発症までの平均日数差分 [院外 - 院内]", main="リサンプリング", nclass=30)
quantile(diff_mean, c(alpha/2, 0.5, 1-alpha/2))

# stan
library(rstan)
library(vioplot)
rstan_options(auto_write=TRUE)
options(mc.cores=parallel::detectCores())

code <- "
  data {
    int<lower=0> N1;
    real<lower=0> y1[N1];
    int<lower=0> N2;
    real<lower=0> y2[N2];
  }

  parameters {
  real<lower=0, upper=20> shape[2];
  real<lower=0, upper=10> scale[2];
  }

  model {
    y1 ~ gamma(shape[1], 1/scale[1]);
    y2 ~ gamma(shape[2], 1/scale[2]);
  }
"

m0 <- stan_model(model_code=code)
standata <- list(N1=n[1], y1=dat[[1]], N2=n[2], y2=dat[[2]])
fit <- sampling(m0, standata, iter=1000, warmup=300, chain=4)
ex <- extract(fit, pars=c("shape", "scale"))
mes <- ex$shape * ex$scale

vdat <- cbind.data.frame(estimate=c(mes), label=rep(lab, each=nrow(mes)))
vioplot(estimate ~ label, data=vdat, col=rev(cols), horizontal=TRUE, at=c(1, 2), side="right",
        xlab="発症までの平均日数", ylab="")
abline(h=c(1, 2), lty=3)
abline(v=shape*scale, lty=3)

apply(mes, 2, quantile, c(alpha/2, 0.5, 1-alpha/2))
diff_mes <- apply(mes, 1, diff)
quantile(diff_mes, c(alpha/2, 0.5, 1-alpha/2))
hist(diff_mes, xlab="発症までの平均日数差分 [院外 - 院内]", main="リサンプリング", nclass=30)


diff_true <- diff(shape*scale)
par(mfrow=c(1, 2))
hist(diff_mean, xlab="発症までの平均日数差分 [院外 - 院内]", main="リサンプリング", nclass=30)
abline(v=diff_true, lwd=3, col="red")
hist(diff_mes, xlab="発症までの平均日数差分 [院外 - 院内]", main="Rstan", nclass=30)
abline(v=diff_true, lwd=3, col="red")