機械学習の評価として、Recall, Precision, F値, Matthews correlation coefficient (MCC)があるので、Rでできる機械学習をひたすらやって性能評価をしてみる。
今回は交差検証は行わず、データセットの全てのデータでモデルを構築して、それを元のデータに戻すだけにする。
で定義される。
Machine Learning Repositoryから、二値分類に使えそうなspam (kernlab) と BreastCanser (mlbench)でやってみる。
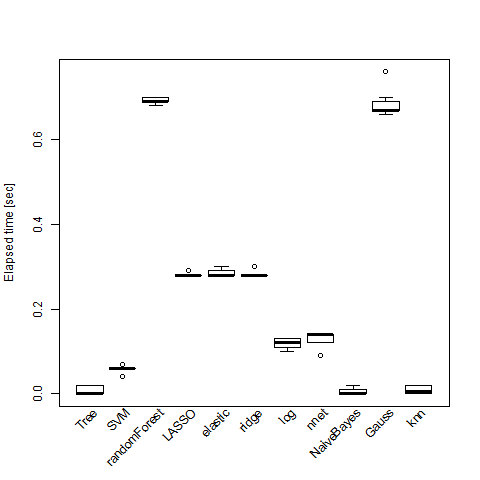
結果としては、とりあえずrandomforestしておけばいいんじゃないかという感じになった。ANNもなかなかよい。Deep learning もここからなんとか勉強したい。
ガウス過程分類はspamのようにサンプルとパラメータが多い時に死ぬほど計算時間がかかるので計算時には注意したい。
もっと真面目になるならパラメータのtuning (SVMやrandomForest)が必要だが、面倒なので割愛!!
# BreastCancer recall precisiion F MMC elapse Tree 0.9623431 0.9623431 0.9623431 0.9420728 0.006 SVM 0.9665272 0.9467213 0.9565217 0.9328627 0.059 randomForest 0.9790795 0.9473684 0.962963 0.9428248 0.691 LASSO 0.958159 0.958159 0.958159 0.9356365 0.282 elastic 0.958159 0.958159 0.958159 0.9356365 0.286 ridge 0.9539749 0.9579832 0.9559748 0.9323578 0.282 log 1 1 1 1 0.119 nnet 1 1 1 1 0.13 NaiveBayes 0.9874477 0.9477912 0.9672131 0.9494842 0.005 Gauss 0.9748954 0.9588477 0.966805 0.9487854 0.682 knn 0.9707113 0.9707113 0.9707113 0.9549455 0.009
# spam recall precisiion F MMC elapse Tree 0.8720353 0.9144014 0.892716 0.8262535 0.116 SVM 0.9167126 0.948089 0.9321368 0.889554 2.478 randomForest 0.9288472 0.9562748 0.9423615 0.9060278 9.752 LASSO 0.8946498 0.9321839 0.9130312 0.8588498 23.202 elastic 0.8913403 0.9308756 0.9106791 0.8551788 23.122 ridge 0.8521787 0.925704 0.887421 0.8208929 4.39 log 0.892995 0.9299253 0.9110861 0.8556405 0.296 nnet 0.9365692 0.9491336 0.9428096 0.9060808 1.068 NaiveBayes 0.9481522 0.5840979 0.7228764 0.5181849 0.176 Gauss 0.9097561 0.9467005 0.9278607 0.8798849 4192.99 knn 0.8769994 0.8867819 0.8818636 0.8057751 1.532
ML.Performance <- function(response, parameter, niter=3){ # response は二値応答ベクトル # parameter は統計量の matrix # niter は計算時間比較のための演算回数 type <- response mat <- parameter input <- na.omit(as.data.frame(cbind(mat, type))) timemat <- matrix(0, nr=11, nc=niter) for(i in seq(niter)){ # Tree library(tree) timemat[1, i] <- system.time(t0 <- tree(type ~ ., data=input))[3] #plot(t0); text(t0) p0 <- predict(t0, input, type="class") r0 <- table(input$type, p0) # SVM library(e1071) timemat[2, i] <- system.time(s0 <- svm(type ~ ., data=input))[3] p1 <- predict(s0, input) r1 <- table(input$type, p1) # randomforest library(randomForest) timemat[3, i] <- system.time(f0 <- randomForest(type ~ ., data=input))[3] r2 <- table(input$type, f0$predict) # LASSO library(glmnet) idx <- which(colnames(input) == "type") hoge <- apply(as.matrix(input[,-idx]), 2, as.numeric) func0 <- function(){ g0 <- glmnet(hoge, input$type, family="binomial", alpha=1) cv0 <- cv.glmnet(hoge, input$type, family="binomial", alpha=1) list(g0, cv0$lambda.min) } timemat[4, i] <- system.time(funcres0 <- func0())[3] r3 <- table(input$type, predict(funcres0[[1]], hoge, s=funcres0[[2]], type="class")) # Elastic Net func1 <- function(){ g6 <- glmnet(hoge, input$type, family="binomial") cv6 <- cv.glmnet(hoge, input$type, family="binomial") list(g6, cv6$lambda.min) } timemat[5, i] <- system.time(funcres1 <- func1())[3] r6 <- table(input$type, predict(funcres1[[1]], hoge, s=funcres1[[2]], type="class")) # ridge idx <- which(colnames(input) == "type") g5 <- glmnet(hoge, input$type, family="binomial", alpha=0) cv5 <- cv.glmnet(hoge, input$type, family="binomial", alpha=0) func2 <- function(){ g5 <- glmnet(hoge, input$type, family="binomial", alpha=0) cv5 <- cv.glmnet(hoge, input$type, family="binomial", alpha=0) list(g5, cv5$lambda.min) } timemat[6, i] <- system.time(funcres2 <- func2())[3] r5 <- table(input$type, predict(funcres2[[1]], hoge, s=funcres2[[2]], type="class")) # glm timemat[7, i] <- system.time(g1 <- glm(type ~ ., data=input, family="binomial"))[3] p4 <- predict(g1, input, type="res") l4 <- replace(rep(levels(type)[1], nrow(input)), p4 >= 0.5, levels(type)[2]) r4 <- table(input$type, l4) # neural net library(nnet) timemat[8, i] <- system.time(n0 <- nnet(type ~ ., data=input, size=3))[3] r7 <- table(input$type, predict(n0, input, type="class")) # naive bayese library(klaR) timemat[9, i] <- system.time(nb0 <- NaiveBayes(type ~ ., data=input))[3] p8 <- predict(nb0, input, type="class") r8 <- table(input$type, p8$class) # Gaussian processing library(kernlab) if(nrow(input) < 1000){ timemat[10, i] <- system.time(g9 <- gausspr(type ~ ., data=input))[3] r9 <- table(input$type, predict(g9, input)) } else { # 計算に時間がかかるので size0 <- c(300, 500, 800, 1000) time1 <- rep(0, length(size0)) for(s0 in seq(size0)){ idx0 <- sample(seq(type), size=size0[s0]) time1[s0] <- system.time(g9 <- gausspr(type ~ ., data=input[idx0,]))[3] r9 <- table(input$type[idx0], predict(g9, input[idx0,])) } lm0 <- lm(log(time1) ~ log(size0)) timemat[10, i] <- exp(sum(lm0$coefficients * c(1, log(nrow(input))))) # spam ならこんな感じで線形回帰に乗る } # k neiberhood library(class) timemat[11, i] <- system.time(k10 <- knn(input[, !colnames(input)=="type"], input[, !colnames(input)=="type"], cl=input$type, k=2))[3] r10 <- table(input$type, k10) } # 統計量を算出する関数 stats <- function(mat){ recall <- mat[2,2]/sum(mat[2,]) precision <- mat[2,2]/sum(mat[,2]) F <- (2*recall*precision)/(recall+precision) MMC <- (prod(diag(mat))-mat[1,2]*mat[2,1])/sqrt(prod(rowSums(mat), colSums(mat))) ret <- list(recall=recall, precisiion=precision, F=F, MMC=MMC) } res <- list(Tree=r0, SVM=r1, randomForest=r2, LASSO=r3, elastic=r6, ridge=r5, log=r4, nnet=r7, NaiveBayes=r8, Gauss=r9, knn=r10) elapse <- rowMeans(timemat) performance <- t(sapply(res, stats)) rownames(timemat) <- rownames(performance) result <- cbind(performance, elapse) boxplot(t(timemat), xaxt="n", ylab="Elapsed time [sec]") text(seq(nrow(timemat)), rep(par()$usr[3], length(nrow(timemat))), rownames(timemat), xpd=TRUE, srt=45, adj=c(1,1)) return(list(result=result, elapsed=timemat)) }