試験問題が多いと大変ですね()

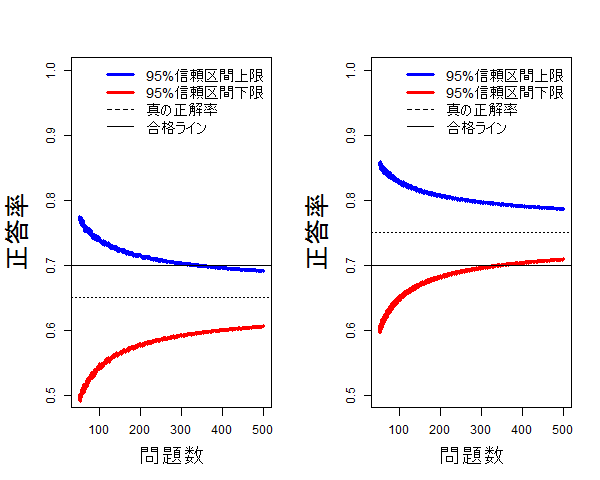
試験問題が多いと受験そのものが大変だということをよく言われるが、実際のところ合格するには問題数が多いほうがいいよね、という話を友人がしていた。
統計学的には、問題数が増えると、受験者が持つ真の正答率に近づくので、勉強をしっかりしている人にとっては、真の実力に近づくため問題数が多いほうがいい。
勉強をしっかりしていない人は、真の実力が合格ラインを超えていないので、真の実力を問われると不合格になってしまう。そのため、問題数が少ないときのランダムな散らばりが合格ラインを超える方向にばらついてくれることを期待して、問題数が少ないほうがいい。
　
問題数が少ないと、実力がある人でも不合格になりうる。いわゆる必修落ちがここらへんのことだろう。

t.ans0 <- c(0.65, 0.75) # 真の正解率
pass.rate <- 0.7        # 試験の合格ライン
alpha <- 0.05           # 有意水準
x <- 50:500             # 問題数

par(mfrow=c(1, 2))
for(t.ans in t.ans0){
	res <- t(mapply(function(x) binom.test(floor(x*t.ans), x, t.ans)$conf.int, x))
	par(mar=c(5, 5, 4, 2))
	matplot(x, res, type="l", xlab="問題数", ylab="正答率", col=c(2,4), lty=1, lwd=3, cex.lab=2, ylim=c(0.5, 1))
	abline(h=pass.rate, lty=1)
	abline(h=t.ans, lty=3)
	legend("topright", legend=c(paste(round((1-alpha)*100), "%信頼区間", c("上限", "下限"), sep=""), "真の正解率", "合格ライン"),
		lwd=c(3,3,1,1), col=c(4,2,1,1), bty="n", lty=c(1,1,2,1), cex=1.2)
}