PK戦での各試行に及ぼす影響をrstan でやってみる - 驚異のアニヲタ社会復帰の予備

MikuHatsune2017-03-07

PK 戦の順序が勝ちやすさに影響するか考えたかったけど、データを集めた時点で先攻が勝つ確率が50% だったので、いろいろな条件のもとでのPK の成功率を考えていた。
stan でやってみる。
　
PK は10人が蹴るまでに終わるとする(154試合1389回)。
各PK での成功率は $p$ である。これが、1人目から10人目までのうち $j$ 番目のキッカーに対して、以下の影響(係数) $\beta$ があるとする。
$\beta_1$ ：切片。他の影響が何もないときの基礎成功率。
$\beta_2$ ：直前の相手の成功(1)/失敗(0) による影響。直前の相手の成功/失敗は $z_{j-1}\in \{0,1\}$ のベルヌーイ試行とする。
$\beta_3$ ：直前の味方の成功(1)/失敗(0) による影響。直前の味方の成功/失敗は $z_{j-2}\in \{0,1\}$ のベルヌーイ試行とする。
$\beta_4$ ：PK の回が進むに連れて受ける影響。 $j$ にそのまま線形に乗ずる。
$\beta_5$ ：そのPK を成功すると勝利、もしくは、失敗すると敗北のフラグに関する影響。そのPK の成功/失敗に関係なく、試合が決まらなければ0、成功した時に勝利するなら1、失敗した時に敗北するなら-1 の値を格納しておく。
というパラメータを用意して、実際の成功率は
$p=\textrm{invlogit}(\beta_1+z_{j-1}\beta_2+z_{j-2}\beta_3+j\beta_4+f_j\beta_5)$
という変換で[0,1] にしておく。ここで $f_j$ は $j$ 番目の選手が蹴るときの勝敗フラグ $\{-1,0,1\}$ である。
PK の成功/失敗は、 $i$ 試合目の $j$ 番目の選手について $z_{i,j}\in \{0,1\}$ なので、
$z_{i,j}\sim \textrm{bernoulli}(p_j)$
とサンプリングされる。
　
R でやるときは、例えば8回目で終わって9,10回目がNA のときを回避するためのidx, 1番目と2番目の選手については、直前の相手(j-1),直前の仲間(j-2) の結果がないので、影響がなくてもいいように0 を無理やりデータにいれてrstan を回している。
　
結果としては、4chain 2000 回ですべて収束した。計算は10秒くらい。

4 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

        mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
b[1]    1.56    0.00 0.16    1.23    1.45    1.56    1.67    1.89  1829    1
b[2]   -0.18    0.00 0.15   -0.47   -0.29   -0.18   -0.08    0.11  2062    1
b[3]    0.10    0.00 0.15   -0.20    0.00    0.10    0.20    0.39  2149    1
b[4]   -0.06    0.00 0.03   -0.12   -0.08   -0.06   -0.05   -0.01  1987    1
b[5]    0.84    0.00 0.16    0.53    0.73    0.83    0.95    1.17  2662    1
lp__ -751.50    0.04 1.60 -755.38 -752.35 -751.15 -750.33 -749.44  1489    1

この結果はinv.logit する前の線形パラメータなので、inv.logit して考える。

             [,1]        [,2]        [,3]         [,4]      [,5]
  2.5%  0.7739358 -0.11624136 -0.04874818 -0.029273129 0.1283631
  50%   0.8267488 -0.04609405  0.02457289 -0.016001107 0.1960369
  97.5% 0.8683126  0.02859455  0.09669435 -0.002499696 0.2622942

基礎成功率は83% だった。
95% 信用区間的に有意なのはPK の順番と勝敗フラグのときだった。PK の順番は効果量が小さいが信用区間が狭く、PK の順番が進むごとに1.6% 成功率が下がる。
勝敗フラグがあるとき、20% 近く確率の変動がある(勝ちフラグは1、負けフラグは-1 なのでそのまま考えてよい)。
直前の相手/仲間の成功は有意ではないとは言え、仲間が成功していたら正の効果(2.5%)、相手が成功していたら負の効果(-4.6%)はある様子。

　
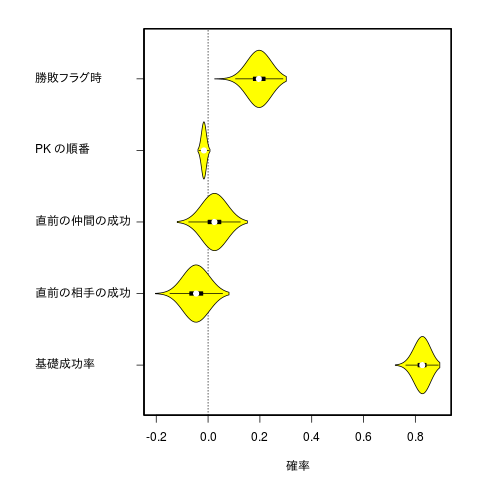
こういう効果を踏まえていろいろ計算すると、全体的な成功率は76% 程度になる。
各回での成功率をプロットすると、PK の順番係数が有意に負なので、全体的にPK の回が進むと、成功率は下がる。
8回目以降で裾が広く、山がふたつあるように見える。10回目に至っては成功率が上がっている。これは勝敗フラグによりふたつの状況が混在しているためにこのようになっている。

そこで勝敗フラグによってPK を分類してそれぞれ成功率をプロットすると、勝ちフラグ時には86%、負けフラグ時には51% の成功率だった。

　
フットボールネーション、いまPK 戦をしていて、3話くらい前にPK 線の確率の話をしていた気がするが、休載が多くて忘れた。

モデル

data{
  int<lower=0> N; # No. game
  int<lower=0, upper=1> PK[12, N]; # result of kick
  int<lower=-1, upper=1> Flag[12, N]; # Win or lose flag
  int<lower=0, upper=12> idx[N];
}
parameters{
  real b[5];
}
model{
  {
    real p;
    p <- inv_logit(b[1] + PK[j-1, i]*b[2] + PK[j-2, i]*b[3] + (j-2)*b[4] + Flag[j, i]*b[5]);
    for(i in 1:N){
      for(j in 3:idx[i]){
        PK[j, i] ~ bernoulli(p);
      }
    }
  }
}

library(rstan)
library(vioplot)
library(gtools)
dat <- readLines("pk.txt")
s <- do.call(rbind, mapply(strsplit, dat, " ", USE.NAMES=FALSE))
s1 <- lapply(mapply(strsplit, s[,3], "", USE.NAMES=FALSE), as.numeric)

# 勝敗が決まりうる番での確率
# すべて書き出す
tide <- function(vec){
  n <- 6:length(vec)
  flag <- rep(0, length(vec))
  for(i in n){
    p1 <- vec[ which(odd(seq(i-1))) ]
    p2 <- vec[ which(even(seq(i-1))) ]
    dif <- sum(p1) - sum(p2)
    if(i == 6){
      if(dif == 3){
        flag[i] <- -1
      } else if(dif == -2){
        flag[i] <- 1
      }
    } else if(i == 7) {
      if(dif == 2){
        flag[i] <- 1
      } else if (dif == -2) {
        flag[i] <- -1
      } 
    } else if (i == 8) {
      if (dif == 2){
        flag[i] <- -1
      } else if (dif == -1) {
        flag[i] <- 1
      }
    } else if (i == 9) {
       if (dif == 1){
         flag[i] <- 1
       } else if (dif == -1){
         flag[i] <- -1
       }
    } else if (i == 10){
      if (dif == 1) {
        flag[i] <- -1
      } else if (dif == 0){
        flag[i] <- 1
      }
    } else {
      if(i%%2 == 0){
        flag[i] <- ifelse(dif==0, 1, -1)
      }
    }
  }
  return(flag)
}

wlflag <- mapply(tide, s1)
a1 <- s1[ sapply(s1, length) < 11 ]
wl1 <- wlflag[ sapply(s1, length) < 11 ]

vec10 <- function(vec) c(vec, rep(NA, 10-length(vec)))
a2 <- rbind(0, 0, mapply(vec10, a1))
wl2 <- rbind(0, 0, mapply(vec10, wl1))
idx <- colSums(!is.na(a2))
a2[is.na(a2)] <- 0
wl2[is.na(wl2)] <- 0

m <- stan_model(model_code=stanmodel)
standata <- list(N=ncol(a2), PK=a2, Flag=wl2, idx=idx)
fit <- sampling(m, standata)
ex <- extract(fit)

# rstan 内でできなかったので計算後に再計算する
p <- matrix(NA, 12, ncol(a2))
for(i in 1:ncol(a2)){
  b <- ex$b[i,]
  for(j in 3:idx[i]){
    p[j, i] <- inv.logit(b[1] + a2[j-1, i]*b[2] + a2[j-2, i]*b[3] + (j-2)*b[4] + wl2[j, i]*b[5])
  }
}
p <- t(tail(p, -2))

plot(0,  0, type="n", xlim=c(1, ncol(p))+c(-1, 1)*0.5, ylim=c(0, 1), xlab="PK 戦の蹴る回", ylab="成功率")
for(i in 1:ncol(p)) vioplot(na.omit(p[,i]), at=i, add=TRUE, col=7)

w <- tapply(c(p), c(t(tail(wl2, -2))), c)
w <- w[-2]
plot(0, 0, type="n", xlim=c(0, 1), ylim=c(1, 2)+c(-1, 1)*0.5, yaxt="n", xlab="成功確率", ylab="")
for(i in seq(d)) vioplot(w[[i]], at=i, add=TRUE, horizontal=TRUE, col=c("blue", "red")[i])
text(par()$usr[1], 1:2, c("負けフラグ", "勝ちフラグ"), pos=4, xpd=TRUE)

r <- sweep(inv.logit(ex$b), 2, c(0, inv.logit(rep(0, 4))), "-")
bcoef <- c("基礎成功率", "直前の相手の成功", "直前の仲間の成功", "PK の順番", "勝敗フラグ時")
par(mar=c(4.5, 10, 2, 2))
plot(0, 0, type="n", ylim=c(1, ncol(r))+c(-1, 1)*0.5, xlim=range(r), ylab="", xlab="確率", yaxt="n")
abline(v=0, lty=3)
for(i in 1:ncol(r)) vioplot(r[,i], at=i, add=TRUE, col=7, horizontal=TRUE, frame=FALSE)
axis(2, 1:ncol(r), labels=NA)
text(par()$usr[1]-0.45, 1:ncol(r), bcoef, xpd=TRUE, pos=4)