

- 作者: 山田亮
- 出版社/メーカー: オーム社
- 発売日: 2010/09/04
- メディア: 単行本(ソフトカバー)
- 購入: 7人 クリック: 155回
- この商品を含むブログ (38件) を見る
分割表といえば、もっとも単純なものは
というもので、周辺度数のe, f,, g, h, n を固定して、各項のa, b, c, d がどんな具合か、を調べる。
Fisher の正確確率検定は、前にもやったけど周辺度数が決まっているときに、考えられる分割表のパターンを列挙して、その生起確率を求める。生起確率は
となる。階乗が含まれるので計算機的には対数をとる。周辺度数が大きくなると取りうる分割表のパターンが増えるので、計算量としては厳しい。しかし、すべての場合の数を網羅するので、正確と言われる。
http://bio-info.biz/tips/r_fisher_test.html
カイ自乗検定は、分割表に対して検定をすれば、2群が独立なのかそれともなんらかの関係をもって各項が分布しているのかを検定するし、1次元ベクトルに使えば、例えばメンデルのアサガオの色的なあれで言えばどれくらい想定している確率に従って分布しているかの適合度検定とかに使われる。これはどちらも、周辺度数(か想定確率)によって各項の期待値というものが計算できて、そこからどれくらいずれているかを定量化してp値にしている。ずれは自乗値で計算されていて、そこから分割表の行と列数に応じた自由度が決まって、カイ自乗分布から統計量→p値への変換がなされる。
各項の値を
となる。
周辺度数が小さいときには
正確確率検定のように、すべての場合の数は計算せず、周辺度数から決まる各
尤度比検定は、比較したいふたつの仮説の尤度比をとって、それがあまりにも偏っていたらその値が大きくなるので、そうなった場合は基準となる仮説を棄却しましょう、という考え。
例えば分割表では、帰無仮説
ふたつの大小を考えるときに、商をとると階乗が打ち消しあって捗るから、
掛け算は対数で足し算になること、対数の掛け算は乗数になることを利用すれば、2倍の対数が自乗っぽくなって、カイ自乗分布に帰着できる。
帰無仮説では、片方の群の確率を決めれば、周辺度数が決まっているのでもう片方も同時に決まるので、自由度は1。一方で、対立仮説では、片方の群を決めても、ふたつの群は別々だろうという想定のもとで検定をしようとしているので、もう片方の確率は決まらない。よってこれも独自に確率を決めなければならず、自由度は2。尤度比検定をしようとするときに、比をとると、自由度が1から2に上がるので、尤度比検定をしようとするときの自由度は2-1=1 である。なので自由度1 のカイ自乗分布を採用する。
尤度比検定は、尤度が定義できて、比較したいふたつの仮説があれば、理論上はなんにでも応用可能である。理論的な部分を含むので、連続的ではあるが、サンプルサイズが小さい時のズレの問題がある。
3つの手法を本的にまとめたものがこちら。
| 検定方法 | 計算量 | 小さいサンプルサイズ | 対称性 | 漸近近似 | 連続・離散 |
|---|---|---|---|---|---|
| 正確確率 | 多 | 保守的・正確 | 非対称 | 正確 | 離散 |
| ピアソン | 少 | 正確確率検定との乖離が大きい | 対称 | 漸近 | 連続 |
| 尤度比 | 少 | 正確確率検定との乖離が大きい | 非対称 | 漸近 | 連続 |
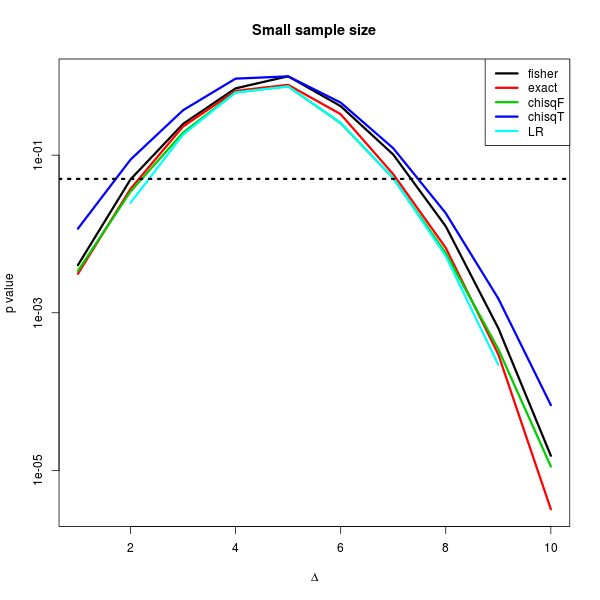
試してみる。横軸はある2*2分割表を入力したときに、自由度1 である項を増減させることができるが、その増減をすべての場合にやり尽くした時の取りうる分割表について、y軸をp値としてプロットしている。
周辺度数が小さい分割表でやってみると、なぜかカイ自乗分布(補正あり)がもっとも大きいp値が返ってきてしまった。横軸の破線はp=0.05 を示しているが、例えば、3つ(にカイ自乗の補正ありなしか、Exact パッケージのexact.test の結果を入れている)の手法でp=0.05 をまたいだりまたがなかったりする瞬間があるわけだが、このときに、尤度比検定をすればもっともp=0.05 を下回りやすいからする、というのはやってはいけないことである。というのは、p-hacking だからである。
であれば、解析を始めるまえから、「尤度比検定を使います」と宣言して、尤度比検定しか使わないのはどうか。これは、個人的にはギリギリ許してあげようかと思う。けれども、「尤度比検定はそもそも小さなp値がでやすい。それすなわち論文になりやすい!」というような邪な考えならば、絶対に許さない絶対ニダ。
統計的な判断は、どんだけ突っ込まれようともスキのない結果を提示すべきだと思っているから、こういうときは保守的(どう頑張っても大きめなp値が出やすい検定なんだけど、それでやってもp<0.05 なんですよ、これなら文句ないでしょ?)な方法を選択しておくのが無難。
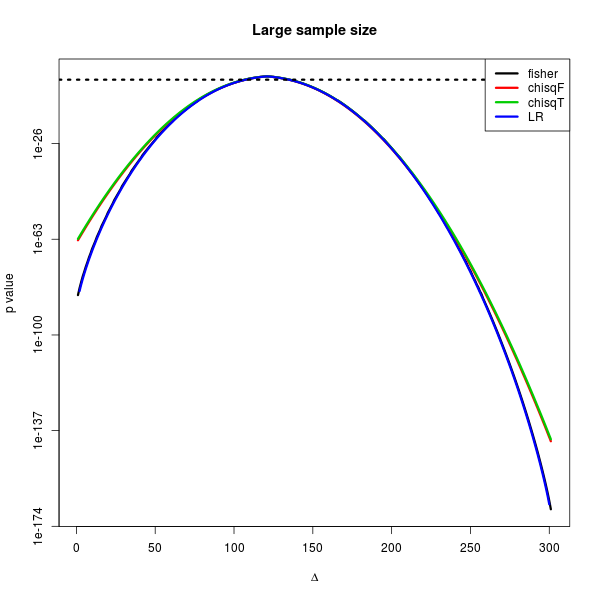
周辺度数が大きな分割表では、もはやp=0.05 のようなチンケな領域においてほとんど手法間に差はない。しかし、分割表がばらついてきて( が0 もしくは大きいところは、入力した2*2 分割表をさらに偏らせた方向に行っているので、ものすごく小さなp値が出やすい)、小さなp値が出ている。この領域では、尤度比検定がものすごい小さなp値を出す傾向にあるようである。しかし、-60 乗のp値ってそんなの誰も気にしない領域だと思うので、まあいいんじゃないかとは思うけど。
library(Exact) mat <- matrix(c(10, 20, 30, 40), 2) # 大きい分割表 mat <- matrix(c(3, 6, 9, 12), 2) # 小さい分割表 # 期待値 makeExptable <- function(mat){ m1 <- margin.table(mat, 1) m2 <- margin.table(mat, 2) N <- sum(mat) etable <- m1 %*% t(m2) / N return(etable) } # 尤度比検定 LR.test <- function(mat){ etable <- makeExptable(mat) chi2 <- 2 * sum(log(mat / etable) * mat) df <- prod(dim(mat) - 1) p <- pchisq(chi2, df, lower.tail=FALSE) return(list(stat=chi2, p.value=p)) } # すべてのとりうる分割表 tabs <- function(mat){ idx <- matrix(c(1, -1, -1, 1), 2) i <- -mat[1,1]:sum(mat) bs <- mapply(function(z) mat + idx*z, i, SIMPLIFY=FALSE) bs[ apply(sapply(bs, ">=", 0), 2, all) ] } # 3つの検定法をすべてのとりうる分割表で試す p_three <- function(mat){ b0 <- tabs(mat) pv <- mapply(function(z) c(fisher=fisher.test(z)$p.value, chisqF=chisq.test(z, correct=FALSE)$p.value, chisqT=chisq.test(z, correct=TRUE)$p.value, LR=LR.test(z)$p.value ), b0) return(list(tables=b0, p.value=t(pv))) } x <- p_three(mat) matplot(x$p.value, lty=1, type="l", log="y", xlab=expression(Delta), ylab="p value", lwd=3) abline(h=0.05, lty=3, lwd=3) legend("topright", legend=colnames(x$p.value), lty=1, col=seq(ncol(x$p.value)), bg="white", lwd=3) title("Large sample size")