検査と臨床判断(担当YF) - 驚異のアニヲタ社会復帰の予備

MikuHatsune2012-11-24

病気である $D^+$ 、病気でない $D^-$
検査陽性である $T^+$ 、検査陰性である $T^-$
としたときに、目の前の患者がある病気である事前確率 $P_{pre}=P(D^+)$ が、検査をすることによってどう上がったり下がったりするかの事後確率 $P_{post}=P(D|T)$ を定量的に考える。
いま、感度 $S_n=P(T^+|D^+)$ 、特異度 $S_p=P(T^-|D^-)$ の検査が陽性となったときの事後確率 $P_{post}=P(D|T)$ は
$P_{post}=\frac{S_nP_{pre}}{S_nP_{pre}+(1-S_p)(1-P_pre)}$
ここで、オッズが $Odds(P)=\frac{P}{1-P}$ となることを考えると、上の式は
$Odds(P_{post})=\frac{S_n}{1-S_p}Odds(P_{pre})$
となる。いま、 $LR^+=\frac{S_n}{1-S_p}$ として、陽性尤度比と定義すると、事後確率は
$P_{post}=\frac{LR^+P_{pre}}{1+P_{pre}(LR^+-1)}$
となるので、これをプロットすると

#事後確率を計算する
Po <- function(Pr, LR){
	(LR * Pr)/(LR*Pr + 1 - Pr)
}
#尤度比
#LR <- seq(0, 30, length=100)
LR <- c(1/10, 1/5, 1/2, 1, 2, 5, 10)
Pr <- seq(0, 1, length=100)
#事後確率の計算結果
Ppost <- matrix(0, length(Pr), length(LR))
for(x in 1:length(Pr)){
for(y in 1:length(LR)){
	Ppost[x, y] <- Po(Pr[x], LR[y])
}}
dimnames(Ppost) <- list(round(Pr, 2), LR)

matplot(Pr, Ppost, type="l", lty=1, col=1:length(LR), lwd=3, xlab="pre probability", ylab="post probability", main="probability trantision by test")
legend("bottomright", legend=paste("LR", LR), bty="n", col=1:length(LR), lty=1, lwd=3)

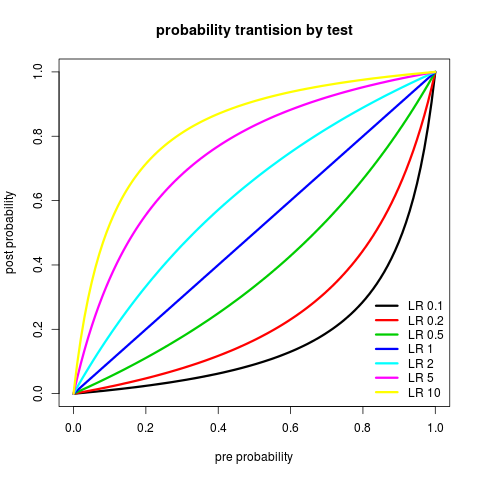
とは言うものの、こんなことを臨床の現場でいちいち計算しているヒマはないため、Steven McGeeというお偉いさんが

Evidence-Based Physical Diagnosis, 3e

作者: Steven McGee MD
出版社/メーカー: Saunders
発売日: 2012/04/02
メディア: ペーパーバック
クリック: 2回
この商品を含むブログを見る

$\begin{matrix}LR&10^{-1}&5^{-1}&2^{-1}&1&2&5&10\\probability&-45%&-30%&-15%&0%&15%&30%&45%\end{matrix}$
ぐらいに相当するんじゃね?ということを言っているらしい。
LR=6とかなったらどうするの?という話には、5よりちょっと大きいくらいだから35%-40%くらいでいいんじゃね?という考えと、
事象が独立なら確率は足してもいいみたいなうろ覚えな数学を持ち出すと、6=2*3→15%+(15%+α)=35%-40%くらいという感じでいけるらしい。
事前確率と事後確率の差をプロットするとこんな感じ。

matplot(Pr, Ppost-Pr, type="l", lty=1, col=1:length(LR), lwd=3, xlab="pre probability", ylab="post probability", main="probability trantision by test")
abline(h=c(-3:3)*0.15, lty=2)
legend("bottomleft", legend=paste("LR", LR), bty="n", col=1:length(LR), lty=1, lwd=3)

　
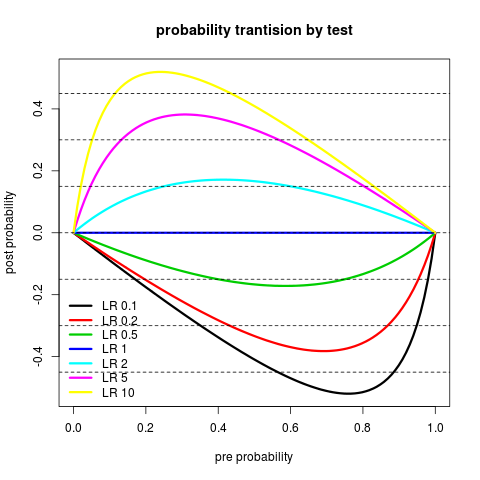
というわけで例題。
あるインフルエンザ迅速診断キットは、感度/特異度が60%/90%らしい。
事前確率がそれぞれ50%, 10%, 80%の場合で、検査が陽性になった場合の事後確率を簡易法と真面目法で計算すると
$LR^+=\frac{0.6}{1-0.9}=6\to +35%$
$\begin{matrix}pre&brief&accurate\\50%&85%&86%\\10%&45%&40%\\80%&100%&96%\end{matrix}$
となり、かなりいい線いく。ノモグラム要らない。
　
40歳男性が急性発症の強い前胸部痛を訴えて来院した。いつもの通り出勤し、仕事を始めたとたんに痛みにおそわれた。その時、特に強い労作はなかったという。以前に１度類似の痛みはあったが、これほどひどくはなく、我慢していると10分ほどで軽快した。今回の痛みは30分以上続いている。170cm、78kg。喫煙歴は１日20本、20年。血圧正常。他に特記すべき既往歴や家族歴はない。
という患者が来た時、おそらく50%くらいで心筋梗塞を疑うだろう。ここで、CKを測定したら、文献的には感度と特異度が
80IUでは93%/87%
280IUでは42%/99%
らしい。陽性尤度比はそれぞれ7.2→40%, 42→70%くらいの上昇。
$\begin{matrix}CK&brief&accurate\\80IU&90%&87.7%\\280IU&100%&97.7%\end{matrix}$
　
次は陰性尤度比を考える。陰性尤度比は上の式を $P_{post}=P(D^-|T^-)$ として求めればいいから、 $LR^-=\frac{1-S_n}{S_p}$ となる。
P1:55歳男性の高血圧患者。労作時に胸骨下の絞扼感を４週間繰り返す。痛みは、あごと左肩から上腕に放散することもある。階段昇降によって生じることが多く、3から5分にて自然軽快する。
P2:30歳男性、これまでは健康で、冠動脈のリスク要因はない。6週間前より、安静時に胸骨下方から上腹部にかけて絞るような痛みが続いていた。痛みは、食後仰臥位で安静時に起こることが多いという。
P3:45歳男性、特に既往歴と冠動脈のリスク要因はない。3週間前より前胸部と胸骨下の疼痛を繰り返す。痛みは刺すような感じだが、時には絞扼感を生じる。労作時にも安静時にも生じる。胸部診察で、胸部肋軟骨部に特に圧痛があるが再現性に乏しい。
という3人の患者が来たとする。このとき、事前確率はそれぞれ90%, 5%, 50%くらいだろうか。
この患者たちに対して、感度と特異度が60%/90%の検査をして、心筋梗塞の可能性がどうなるか考えたい。
陽性尤度比は6→+40%, 陰性尤度比は0.44→-20%くらいと考えられるので、
$\begin{matrix}patient&pre&positive&negative\\P1&90%&99.9%&70%\\P2&5%&45%&0.01%\\P3&50%&90%&30%\end{matrix}$
　
真面目に計算すると
$\begin{matrix}patient&pre&positive&negative\\P1&90%&98.2%&80%\\P2&5%&24%&0.023%\\P3&50%&85.7%&30.8%\end{matrix}$
事前確率が極端に高いP1と低いP2では、事後確率の変動があまりない。検査をするのが有用なのは、P2みたいな中途半端で困る場合。
　
さて、尤度比を考えると、よくあるSpPIn SnNOutがよくわかる、と思う。
$LR^+=\frac{S_n}{1-S_p}$ において、 $S_p$ が1に近づけば近づくほど、 $LR^+$ は大きくなる。
ということで、特異度が高い検査が陽性だと、確定に近づく。(Specificity positive rule In)
$LR^-=\frac{1-S_n}{S_p}$ において、 $S_n$ が1に近づけば近づくほど、 $LR^-$ は小さくなる。
ということで、感度が高い検査が陰性だと、除外に近づく。(Sensitivity Negative rule Out)
　
今回の話は、K病院のT先生のレクチャーを元に構成されています。T先生ありがとうございました。
　
バックナンバー