塩基配列のComplexityとしてエントロピーという統計量を使うのだが、このエントロピーの定義が自分の周辺で物議を醸している。
一般的なシャノンエントロピーは
だが、前の論文では、HBVのquasispeciesとして、クローン数が全部で個の配列で、配列
が
の割合で存在しているとすると
となる、と書いてある。
は、各塩基位置において、AGCTがどの頻度で出現しているかを計算している。
は、各(臨床)サンプルにおいて、ある配列をもつクローンがどの頻度で出現しているかを計算している。
と思う。
で、これらが一致するかという質問を受けたのだが、結論から言うと一致しない。
は、取りうる要素数が
(塩基)のとき、
となる。
は、
未検証。が
となるので、
(エントロピーを自然対数で計算しなおせば)で割れば
になる。
library(MCMCpack) p1 <- rdirichlet(10000, rep(1, 4)) plot(sort(rowSums(-log(p1, 2) * p1)), ylab="Entropy")

例えば、10塩基長、15クローンのデータがあったとして、このデータのシャノンエントロピー()となる。
各塩基でのエントロピーは、総和が2.65で平均が0.265なので、どうすれば一致するんだろうか。たぶんしない。
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [1,] "T" "A" "T" "C" "G" "C" "T" "A" "A" "G" [2,] "T" "A" "T" "C" "G" "C" "T" "A" "A" "G" [3,] "T" "A" "T" "C" "G" "C" "T" "A" "C" "G" [4,] "T" "A" "T" "C" "G" "C" "T" "A" "A" "G" [5,] "T" "A" "T" "C" "G" "C" "T" "T" "A" "G" [6,] "T" "A" "T" "C" "G" "C" "T" "A" "G" "G" [7,] "T" "A" "T" "C" "G" "C" "T" "A" "A" "G" [8,] "C" "A" "T" "C" "G" "C" "T" "A" "A" "G" [9,] "T" "A" "T" "C" "G" "C" "T" "A" "A" "G" [10,] "T" "A" "T" "C" "G" "C" "T" "A" "A" "G" [11,] "T" "A" "G" "C" "G" "C" "T" "A" "A" "G" [12,] "T" "A" "T" "C" "G" "C" "T" "A" "A" "G" [13,] "T" "A" "T" "C" "G" "C" "T" "A" "A" "G" [14,] "T" "A" "T" "C" "G" "T" "T" "A" "T" "G" [15,] "T" "A" "T" "C" "G" "C" "T" "A" "C" "G"
library(seqinr) library(bio3d) bp <- 10 clone <- 15 niter <- 1000 base <- c("A", "G", "C", "T") par(mfrow=c(1, 2)) for(m0 in c(5, 50)){ mut_bases <- rpois(1, m0) res <- matrix(0, niter, 2) for(i0 in seq(niter)){ s1 <- sample(base, size=bp, replace=TRUE) m1 <- mapply(rep, s1, clone) mut <- sample(seq(length(m1)), mut_bases) mutbase <- sample(base, size=length(mut), replace=TRUE) m2 <- matrix(replace(c(m1), mut, mutbase), nr=clone) #AGCTベースのエントロピー Sn_p1 <- mapply(function(x) table(factor(m2[ ,x], levels = base)), seq(bp)) / clone Sn1 <- -colSums(Sn_p1 * log(Sn_p1, 2), na.rm=TRUE) names(Sn1) <- seq(bp) #barplot(Sn1, ylim=c(0, log(length(base), 2)), xlab="base", main="Shannon entropy") #クローンベースのエントロピー seq0 <- table(apply(m2, 1, paste, sep="", collapse="")) Sn2 <- -(seq0 / clone) * log(seq0 / clone) / log(clone) res[i0, ] <- c(mean(Sn1), sum(Sn2)) } xl <- yl <- range(0, res) plot(res, xlim=xl, ylim=yl, cex=0.7, xlab="Base", ylab="Clone") title(paste("Correration of Shannnon entropy\nMutation in", round(m0/(bp*clone) * 100, 1), "% in sequence")) abline(lm(res[, 2] ~ res[, 1])) }
あるひとつの配列中で、変異する塩基が増えると、クローンのシャノンエントロピー()はある定数に近づくようである。

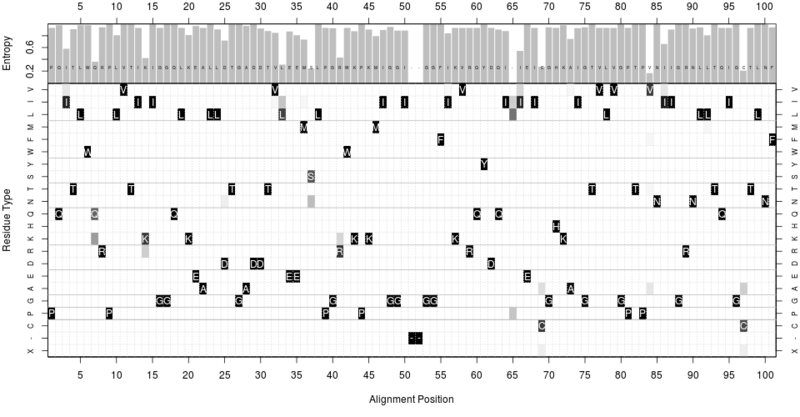
bio3dパッケージにあるentropy関数は、塩基エントロピー()で計算しているようである。
このなかのサンプルデータとして、HIVのプロテアーゼのどっかの領域にひっかかる。
protein BLASTより、データの1行目
PQITLWQRPLVTIKIGGQLKEALLDTGADDTVLEEMSLPGRWKPKMIGGI--GGFIKVRQYDQILIEICGHKAIGTVLVGPTPVNIIGRNLLTQIGCTLNF
を検索すると出てくる。
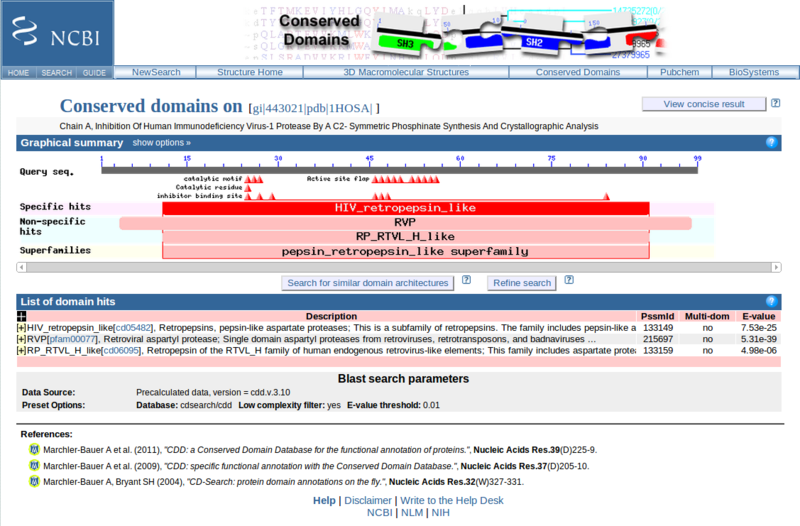
これのサンプルコードを実行すると、いろいろ計算して描いてくれるが、各アミノ酸残基でのエントロピーを計算している。
# Read HIV protease alignment aln <- read.fasta(system.file("examples/hivp_xray.fa",package="bio3d")) # Entropy and consensus h <- entropy(aln) con <- consensus(aln) names(h$H)=con$seq print(h$H) H <- h$H.norm col <- mono.colors(100) aa <- rev(rownames(h$freq)) oldpar <- par(no.readonly=TRUE) layout(matrix(c(1, 2), 2, 1, byrow = TRUE), widths = 7, heights = c(2, 8), respect = FALSE) # Plot 1: entropy par(mar = c(0, 4, 2, 2)) barplot(H, border="white", ylab = "Entropy", space=0, xlim=c(3.7, 97.3),yaxt="n" ) axis(side=2, at=c(0.2, 0.4, 0.6, 0.8)) axis(side=3, at=(seq(0, length(con$seq), by=5) - 0.5), labels=seq(0, length(con$seq), by=5)) box() # Plot2: residue frequencies par(mar = c(5, 4, 0, 2)) image(x=1:ncol(con$freq), y=1:nrow(con$freq), z=as.matrix(rev(as.data.frame(t(con$freq)))), col=col, yaxt="n", xaxt="n", xlab="Alignment Position", ylab="Residue Type") axis(side=1, at=seq(0,length(con$seq), by=5)) axis(side=2, at=c(1:22), labels=aa, cex.axis=0.7) axis(side=3, at=c(1:length(con$seq)), labels =con$seq, cex.axis=0.4, tick=0) axis(side=4, at=c(1:22), labels=aa, cex.axis=0.7) grid(length(con$seq), length(aa)) box() for(i in 1:length(con$seq)) { text(i, which(aa==con$seq[i]),con$seq[i],col="white") } abline(h=c(3.5, 4.5, 5.5, 3.5, 7.5, 9.5, 12.5, 14.5, 16.5, 19.5), col="gray") par(oldpar)