
読んだ。BMC Cell Biology201011:24
細胞の移動追跡を自動化してやってくれるソフトウェアTime Lapse Analyserの話。
マニュアルでやると細胞全体はもちろんチェックできないし、代表的な20細胞を選んでtracking してもらったら軒並みAMD (average mean distance, 細胞集団全体でどれくらい移動距離があるか)が過大評価傾向にあると。
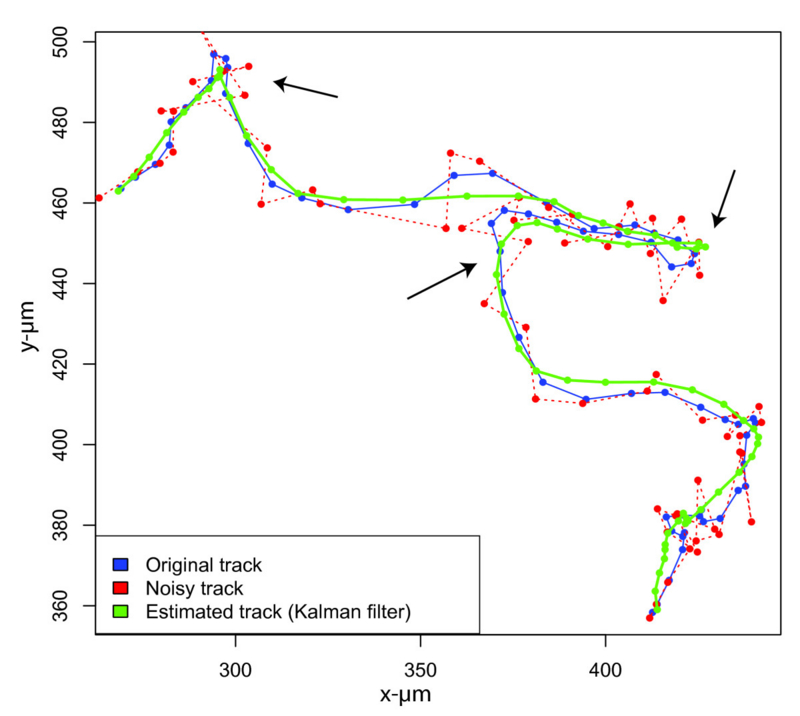
細胞の動いた筋道の推定には、各写真での細胞位置をnearest neighbor でつなげて、ジグザグな動きをKalman filterで平滑化しながら、いい感じの線を推定する。
論文のFigure 3 を完全再現する勢いでやってみる。
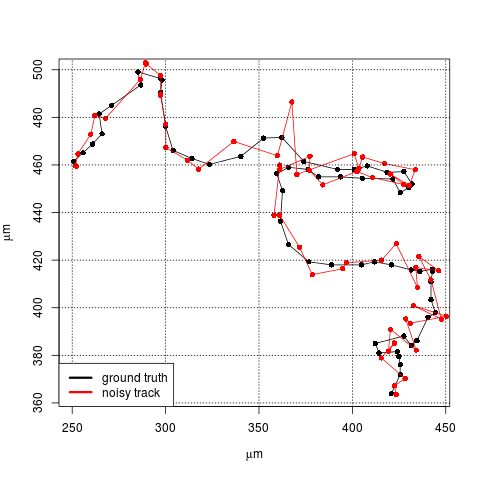
時刻ごとの細胞のxy 座標データがあるとする。黒線は真の線(ground truth というらしい)で、赤線はxy 両方向に適当な、正規分布にしたがう誤差を入れた観測値、という感じ。
時刻の細胞のx 座標
と、そのときの速度
, y も同様にあわらす事にして、Kalman filter は状態
と観測
について
:状態方程式
:観測方程式
と書ける。
今回の細胞の軌跡は、レーダーとかGPS とかそんな感じでやりたいから、こちらを参考に4次元ベクトルに対応するように
:状態方程式
:観測方程式
ここで、,
である。
上の式でほしいのは、乱雑項を与える4*4 の対角行列である,
である。これらは下のfkf でのHHt, GGt に相当する。
これらの推定はこちらを参考に、optim で行う。
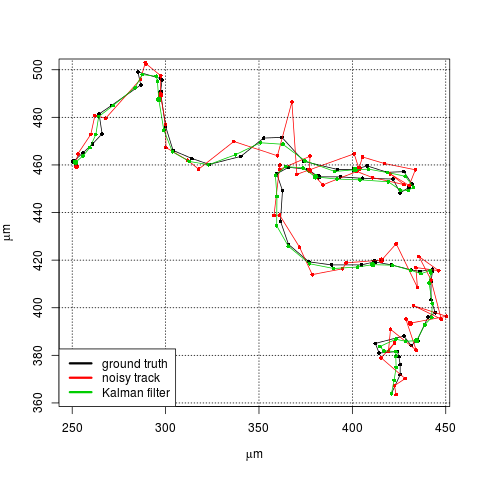
というわけで推定結果がこちら。
fit.fkf$par
で返ってくるのは2乗された値なので、いい感じのときはsqrt を取れば最初に設定した の値に近そうな値が返ってくる。
概ね、カルマンフィルターの推定軌跡はいい感じ。
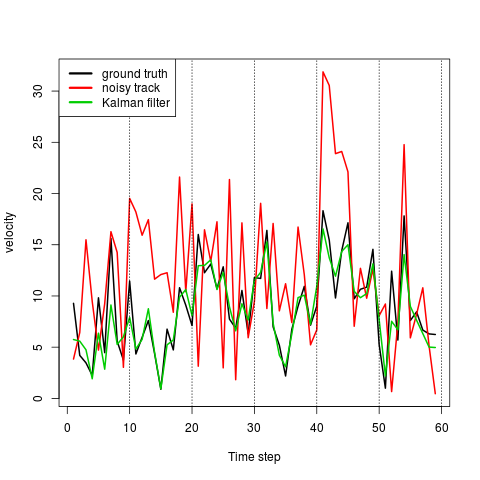
速度についても、例えば右下から出発して上に行った10点目くらいのところで、x軸方向に非常にジグザグしているが、このときの移動距離が過大評価になって非常に大きくなっている。が、カルマンフィルターをやると速度が真の軌跡に近くなっている。
xy0 <- read.table("kf.txt") # 真の位置 s <- 5 # 観測誤差 xy1 <- xy0 + rnorm(length(unlist(xy0)), mean=0, sd=s) # 観測データ # 座標の時間微分が時速 delta_t <- 1 s1 <- (tail(xy1, -1)-head(xy1, -1))/delta_t s1 <- rbind(s1, tail(s1, 1)) Tt <- rbind(c(1,1,0,0), c(0,1,0,0), c(0,0,1,1), c(0,0,0,1)) Zt <- diag(1, 4) dt <- ct <- matrix(1, 4) yt <- rbind(xy0[,1], s1[,1], xy0[,2], s1[,2]) a0 <- yt[,1] P0 <- diag(0.01, 4) library(FKF) delta_t <- 1 # objective function objective <- function(par, ...){ -fkf(HHt = diag(par[1], 4), GGt = diag(par[2], 4), ...)$logLik } ## Estimate parameters # 初期値はある程度予想されそうな値に近そうなところを入れられたら入れる fit.fkf <- optim(c(HHt = 1, GGt = 1), fn = objective, yt = yt, a0 = a0, P0 = P0, dt = dt, ct = ct, Zt = Zt, Tt = Tt) ## Filter data with estimated parameters: mat <- mapply(diag, x=sqrt(fit.fkf$par), ncol=4, nrow=4, SIMPLIFY=FALSE) fkf.obj <- fkf(a0, P0, dt, ct, Tt, Zt, HHt = mat$HHt, GGt = mat$GGt, yt = yt) xy2 <- t(fkf.obj$att[c(1,3),]) # カルマンフィルター後の位置 # 10 点ごとに大きさを変えてプロットする cex0 <- replace(rep(0.7, nrow(xy0)), (1:(nrow(xy0)%/%10))*10, 1) plot(xy0, type="n", xlab=substitute(mu*"m"), ylab=substitute(mu*"m")) lines(xy0, type="o", cex=cex0, pch=16) lines(xy1, type="o", cex=cex0, pch=16, col="red") lines(xy2, type="o", cex=cex0, pch=16, col="green3") abline(h=seq(360, 500, 20), v=seq(250, 450, 50), lty=3) legend("bottomleft", legend=c("ground truth", "noisy track", "Kalman filter"), col=c("black", "red", "green3"), lty=1, lwd=3, bg="white") # 速度 s <- mapply(function(z) sqrt(rowSums(((tail(z, -1)-head(z, -1))/delta_t)^2)), list(xy0, xy1, xy2)) matplot(s, type="l", lty=1, lwd=2, col=c("black", "red", "green3"), xlab="Time step", ylab="velocity") abline(v=(1:(nrow(xy0)%/%10))*10, lty=3) legend("topleft", legend=c("ground truth", "noisy track", "Kalman filter"), col=c("black", "red", "green3"), lty=1, lwd=3, bg="white")
420.9 363.9 425.6 371.9 425.6 376.1 424.9 379.5 424.1 381.6 414.3 381 412.3 385 427.6 388.1 431.5 384.1 434.6 386.2 440.5 396 444.4 397.9 442.1 403.4 442.1 411 442.9 415.3 442.9 416.2 436.2 415.3 431.5 415.9 420.9 418 411.9 419.3 404.9 418 388.9 418 376.7 419.3 365.8 426.6 361.5 436.4 362.6 449.2 359.5 456.3 365.8 459 376.3 458.1 381.8 455 393.6 455 405.3 454.4 421.7 454.1 425.6 448.3 430.3 450.5 431.9 452 427.6 457.2 418.6 456.9 408 459.6 401 458.1 392 458.1 374 461.5 362.3 471.6 352.5 471.3 340.3 463.6 323.5 460.2 314.1 462.7 304 466.1 300 476.2 297.3 490.5 298.1 495.7 297.3 496.3 285.2 499.1 286.7 493.6 271.1 485 264.4 481.4 266 473.1 260.9 468.8 255.8 465.1 250.7 461.5